Fundamentals of the Particle In Cell Method

Overview

This eight-week online course will teach you how develop electrostatic plasma simulation codes using the Particle In Cell (PIC) method. PIC is a popular numerical approach used to simulate plasmas, rarefied gases, and other processes marked by departure from continuum. It represents the gas as a collection of simulation macroparticles, allowing the method to resolve the local velocity distribution function self-consistently. These particles move in a domain covered by a computational mesh, and the mesh is used to compute self-induced forces and inter-particle interactions. In the course, we will develop 1D, 3D, and 2D axisymmetric ES-PIC codes operating on Cartesian meshes. We will also learn about handling surface interactions, modeling ion-neutral collisions, and data post-processing. The more complex electromagnetic and finite element, unstructured mesh PIC codes are covered in the follow-on Advanced PIC course. Material from this course covers material from chapters 1 through 4 in Plasma Simulations by Example. The class will run from May 21st to July 30th, 2024, with a 3 week break between classes 4 and 5 due to conference travel. This should give you time to catch up on homework assignments!

Course Objectives

At the end of the course, you should have a solid understanding of the PIC method and be able to develop your own 1D, 2D, and 3D plasma simulation codes for modeling cases in which the magnetic field is either not present, or does not change with time. You should also be able to: 1) write a solver for plasma potential, 2) model electrons using a simple fluid model, 3) include surface interactions, and 4) model multi-species gases including neutral interactions. The course will also cover post-processing and data visualization.

Course Format

The course consists of online lessons conducted through GoToMeeting. The lessons are recorded and the videos, along with pdf slides and code examples, are posted online shortly after each lesson. The course also includes optional homework assignments, which need to be completed in order to receive a certificate of completion.

Class Schedule

• Lesson 1 – May 21, 2024 (Introduction): We start the course by discussing the difference between fluid and kinetic codes. We then cover the fundamental equations governing electrostatic plasmas and see how they are implemented in the Particle In Cell method. We then develop a basic particle integrator using the Leapfrog scheme and learn how to solve Poisson’s equation using the Finite Difference.
• Lesson 2 – May 28, 2024 (1D Sheath): In this lesson we start developing a 1D fully-kinetic PIC code for modeling formation of the plasma sheath. The first version with stationary particles allows us to discuss numerical noise.
• Lesson 3 – June 4, 2024 (Boundaries, Velocity Sampling, Magnetic Confinement): We complete the 1D sheath simulation by loading thermal particles and including walls. We also discuss symmetry, direct solvers, and secondary electron emission. We then learn about several important concepts such as random number generators, sampling of the velocity distribution function, and the Boris method for integrating particle velocities in the presence of a magnetic field. We use it to simulate a magnetic mirror.
• Lesson 4 – June 11, 2024 (Grounded Box): In this lesson we introduce 3D ES-PIC simulations by developing code modeling electron oscillation in a grounded box. We learn how to perform particle-mesh interpolation in 3D and also learn how to output and visualize results using Paraview.
• No class weeks of June 17 to July 2nd due to SCTC and IEPC conferences
• Lesson 5 – July 9, 2024 (3D Flow past a Sphere): We modify the code from Lesson 4 to simulate flow of plasma past a sphere at a fixed potential using a hybrid 3D ES-PIC. We use this code to introduce sugarcubing and the Boltzmann electron model.
• Lesson 6 – July 16, 2024 (Multiple Species, Visualization, Collisions, and Surface Interactions): We modify the code from the previous lesson by adding a surface impact handler to model surface neutralization. We include neutrals and learn how to simulate particle collisions using the Monte Carlo Collisions (MCC) method. We discuss data averaging and we add additional output options to generate particle traces and phase plots.
• Lesson 7 – July 23, 2024 (Potential Solvers, Mesh, and Virtual Probes): In this lesson we develop a new field solver based on Newton-Raphson and PCG. We also discuss mesh stretching and illustrate sampling data for experimental comparison using virtual Faraday and RPA probes.
• Lesson 8 – July 30, 2024 (Axially-symmetric flow): In the final lecture, we learn how to develop two-dimensional (XY) and axially symmetric (RZ) codes. We mainly focus on the latter, and illustrate the approach by simulating a simplistic ion gun.

Examples

Below are some examples of course materials from 2015:

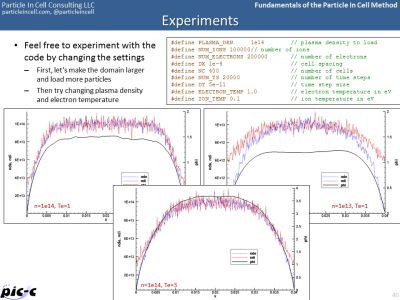
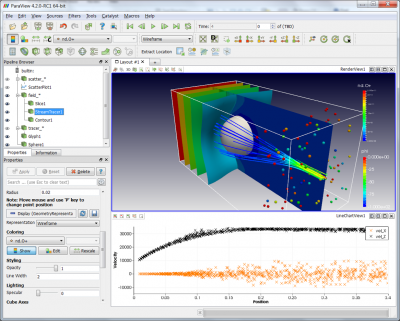
Assignments

• Homework 1 is a numerical simulation of a ball falling under the action of gravity and aerodynamic drag using Leapfrog and Runge-Kutta 4 methods. It also asks you modify a Poisson solver from the lecture to compute electric field and compare it against theory.
• Homework 2 asks you to include additional diagnostics in the developed 1D sheath code. Specifically you should compute node-averaged stream velocities and temperatures. It also asks you to compare the numerical sheath solution to Langmuir’s model and gives you a chance to study the effect of the high velocity tail on secondary electron emission.
• Homework 3 involves simulating ExB drift giving you a chance to see that it is indeed independent of particle’s charge or mass.
• Homework 4 asks you to modify the 3D code to model flow of plasma past an infinitely long cylinder, giving you a 2D solution. You will also write code for mesh-based velocities and data averaging and get to develop your own Poisson solver.
• Homework 5 is a fun project in which you develop from scratch a fully kinetic 3D PIC code to simulate electrons bouncing around in a box of constant density ions.
• Homework 6 gives you a chance to simulate the flow of plasma past a sphere using a 2D axisymmetric code

Instructor

The instructor, Dr. Lubos Brieda, is the founder and president of Particle In Cell Consulting, LLC, a Los Angeles-based company specializing in providing tools and services for the plasma physics and rarefied gas communities. Dr. Brieda has over 10 years of experience developing PIC codes for a wide range of applications, including electric propulsion, space environment interactions, surface processing, and plasma medicine. In addition to his work through PIC-C, Dr. Brieda also teaches scientific computing and computational plasma physics at the Department of Astronautical Engineering at the University of Southern California. He is the author of two textbooks: Plasma Simulations by Example, and Introduction to Modern Scientific Programming and Numerical Methods.

Requirements

All students are expected to have a basic understanding of numerical techniques, plasma and gas dynamics, and computer programming. The lectures and demonstration programs will utilize C++ and Python programming languages. Students need to have access to a computer with a compiler of choice. Computer with Internet access will be needed to access the lectures and course material. The course will be conducted in English.

Register now!