Surface Erosion

We can break the erosion algorithm down into three steps:

1. Determine incoming flux to a surface element
2. Calculate amount of sputtered material
3. Move each node associated with the surface element

Determine Incoming Flux to a Surface Element

Calculating the actual flux of something like a thruster is out of the scope of this article, but we can still do a little work. Given a certain uniform incoming flux into the domain, we need to get the cross sectional area of a surface element that sees that flux. You might be thinking that this is just a simple dot product, and you would be correct. We simply dot the surface normal unit vector with the flux unit vector to give us an area ratio. This ratio multiplied by the element area gives us the cross sectional area visible to the flux. We then get the overall flux to the surface element. I’m sure you are saying “if you had not made the flux a unit vector and just left it with a magnitude then you wouldn’t have to multiply by flux at the end, it would be just the dot product.” That is true, but it is a little easier to visualize if we take small steps!

$$\vec{F_{visible}}=\vec{F_{total}}\cdot \hat{N}$$

Calculating Amount of Sputtered Material

Sputter yield is essentially the number of surface molecules kicked off for each incident molecule. There are a number of algorithms out there to calculate sputter yield and that I am not going to get into. What I will say is that most of them typically take the form of: one function to determine the sputter yield at normal incidence and another to adjust that for incidence angle.

$$Y=f(\text{materials}, \text{flow params})g(\theta, \text{materials})$$

What this tells us is that for a given input flux, F, we will be sputtering away X amount of material. While some models can be extremely complex, a simple cosine model goes a long way – choose a max energy the normal incidence, and a max angle (this is typically NOT at normal incidence, for a first cut 45 degrees is not a bad guess for the peak.) So for our simple model, we may have something like:

$$Y=\cos(E/E_{peak})\cos(\theta + \dfrac{\pi}{2})$$

The peak energy varies wildly by material, but just to try things out, maybe put a few thousand eV in there. If you are really cool, you can model where this sputtered material goes (“please don’t land on the optics!”), but that is a task for another day.

Move each node associated with the surface element

Moving the nodes is the hard part. In reality, each surface interaction only knocks out a molecule or two of material, but we need our sim to run fast so we take off big chunks at a time. And of course by “take off big chunks” what we really mean is move the surface nodes to a new position. So how do we know where to move the nodes?

Let’s take our circle and introduce a uniform flux coming in from the top as shown in Figure 2. To illustrate the effects on the surface we are going to use a laughably coarse mesh, which you would never use in real life, right?

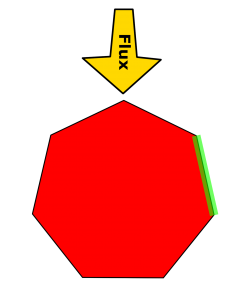
Typically we have small panels and small timesteps so it is OK to just loop through the panels and erode them one by one. For this example we want to erode the surface panel highlighted in green. We know how much material we want to remove, we know the density of the material, and we know the area of the panel, so it should be fairly straightforward to say “OK, my density is 1000 kg/m^3, I want to take out 1e-4 kg, and my area is 5e-2 m^2, soooooooo, if I move the panel in 2e-6 m then I should be all set!” The hard part is what do we mean when we say “move the panel in?” Figure 3 outlines some possible scenarios.

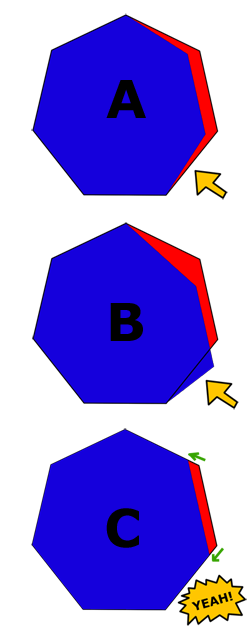
The first place most people would go is to just move along the surface normal. This is shown in Case A. For a very small amount of erosion this would probably be OK, but in our super exaggerated example you can see that the underside of the circle begins to lift up, implying that there is “erosion” on the bottom surface where this is no impingement.

So then you might think a beam of particles is sort of like a drill so maybe we should erode in the direction of the flux. This case is shown in Case B. This makes physical sense, but as shown here, if we move the nodes in the direction of the flux we can actually add material to the surface, which is right out.

OK, so maybe we can move surface nodes along the plane of a neighboring surface. This way we are removing material from this element without affecting any other elements. This technique is shown in Case C. At first this seems like a super deal, but what about the case where we have a flat plate? The nodes would simply slide around on the surface and no erosion would actually occur. HMMMMMMM.

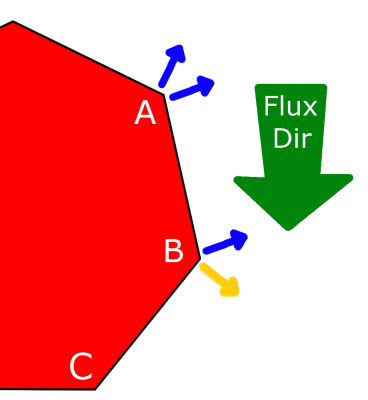
What we really need is a combination of methods B and C. This is shown in Figure 4. We basically want to move a node in the flux direction until it hits a surface, and then move it along the surface. As with most problems in life, this one is again solved by dot products. If the surface normal has a component opposite the flux direction, then that surface is OK to move in the flux direction. But remember, we don’t generally move surfaces, we move nodes. So, when we are moving a node you have to check the normal of both surfaces connected to that node. If they both have a component opposite the flux, then we can move in the flux dir, such as in point A. For point B, however, the yellow arrow dots positively with the flux (has no opposite component), so we have to move point B down the relevant surface.

Now would be a good time to discuss the inherent conflict here between nodes and elements. It is easy to say a particle hits element X, which has an area of Z. It is also easy to move node A in direction B. As we saw above, however, it is a little tougher to have particles hit an element and then translate the nodes. One way to deal with this is to do everything relative to the nodes. What this means is that instead of looping over elements, we actually want to loop through nodes. We say that the “area” of the node, is just half the area of each neighboring element. Calculating both elements is really not that much more work, and it is nicer in a few ways:

• Each node only gets moved once. When we loop through panels, each node gets moved twice, which can get confusing quickly.
• Looping through nodes is much more natural as we already often loop through nodes for other reasons (potential for example)
• If we loop through elements, the normal vector of the element remains ~ constant. This may seem like a good thing, but it restricts the surface from reshaping itself which can lead to some very large or small elements. Looping through nodes gives the mesh a little more freedom to adapt to the imposed shape changes.

Now that we know the direction to move the nodes how far do we move them? We can go back to that same simple thought from before about the density and the volume of material we want to remove. Let’s firm that up a bit:
$latex dx=dfrac{m}{rho Delta y Delta z}$

Our case here is 2D so we can throw out $latex Delta z$.
$latex dx=dfrac{m}{rho Delta y}$

And that is that….. if you are looping through surfaces. This is the one area where looping through the nodes is actually a little tricky as we are no longer just eroding out a rectangle, we are changing the shape of the mesh. Who knows how much volume we are taking out?

As it turns out, it is not as complicated as it might seem. We know the position of all the nodes so you can just look at the node of interest and the neighboring two nodes and treat those three points as a triangle. There are a few ways we can handle this.

• Actually calculate the area of the two triangles and solve for the distance to move. This is the most correct, but is a bit of a pain.
• Assume that, for calculating the distance, the erosion is normal to the triangle baseline. In this case we can just use the change in area of moving a node.$latex Delta A = dfrac{1}{2}bh_1 – dfrac{1}{2}bh_2$
• Since moving this node removes material from two panels, we need to add their areas together when deciding how far to move the node.$latex Delta h = dfrac{2Delta A}{b_1+b_2}$
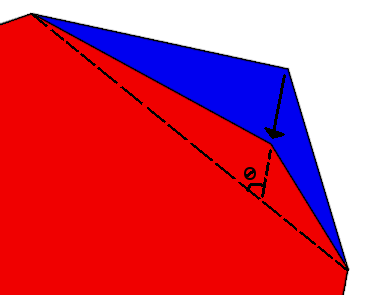
• If you would like to account for the fact that the erosion direction is not strictly along the “h” vector, that is easily done via the angle between the baseline (vector between baseline and the flux direction, as shown in Figure 5.)$latex Delta x = dfrac{Delta h}{sintheta}$

Now that we know how to handle a single erosion event, all we have to do is throw in a couple for loops (elements and time) and start eroding!

Matlab Example

Here is a quick Matlab erosion routine you can try out yourself. It has some default values for all the material stuff and all you specify are the number of sides on the circle and the time. Let’s look at two example runs of this code.

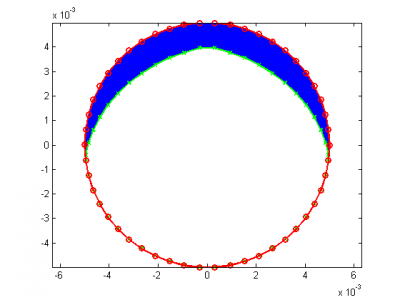
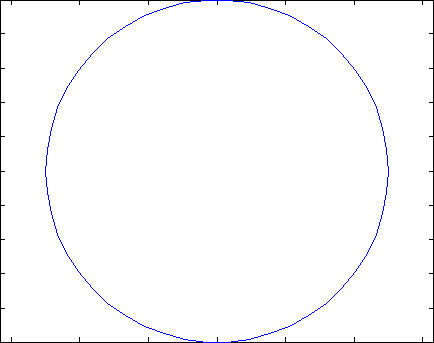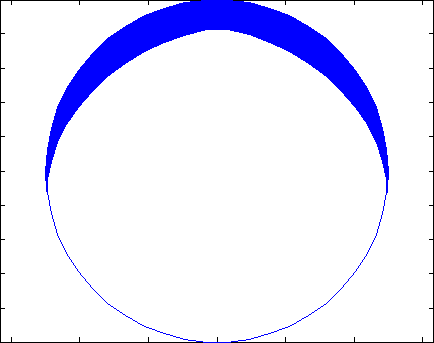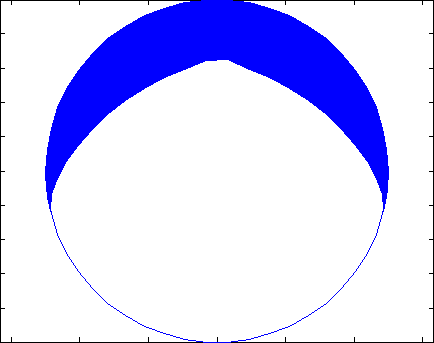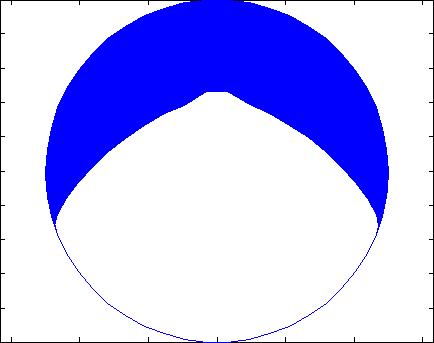
First, we run with our laughably coarse 7 panel circle, run for 2e6 seconds. The result is shown in Figure 7. Note that the nodes all move in the flux direction except for the lower left node, which was forced to move along the surface. Other than this, however, it is tough to really get much out of this since so few panels were involved. It is difficult to say where the max erosion occurred or what shape the final rod will take.

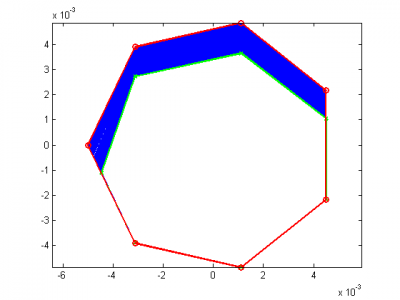
Let’s look at Figure 8, which shows the same 2e6 seconds, but now with 50 panels. Here, the rod is much more symmetrical and now has a definite shape to it – we see that the rod has started to become less circular and more pointy. This makes sense because of our cosine angular profile. Putting in more complex flux distributions or geometries can yield some interesting results!

Here is an animation showing the progression of the erosion. Notice how the top of the circle tends to stay flat because this is a single element. This may be somewhat unrealistic, and could be alleviated by mesh refinement, or element splitting, which will be covered in a separate tutorial.

For more on this, checkout the new online sputter calculator.