Computing Intersections Between a Cubic Bezier Curve and a Line

Introduction
Last week I was running a Starfish simulation of a molecular transport through a vent. Starfish was designed to support both linear and cubic spline representation of surfaces. But while testing the code by tracing particles, I noticed that the particle hits with curved surfaces were not being computed correctly. Digging deeper I found the issue: I never implemented the algorithm for finding intersection between a cubic and a line! Instead, the code was using the line-line intersection by connecting the two end points of the curve. Oops!
Before continuing, let me just say that I am really starting to enjoy algorithm development using interactive HTML technologies! In the past, I would write the code in Java or C++ and have it output the splines and intersection points to a file which I would subsequently visualize using some plotting program. Or using Matlab, I could do the plotting right from the program. But I would still be confined to testing just a single case. With HTML, we can do something much better: we can interactively manipulate the curves and see the algorithm respond in real time!
Demo
You can try this out in the demo above. If everything loaded fine, you should see a blue cubic Bezier curve and a red line. You will also see two white circles, these are the two control points \(\mathbf{P}_1\) and \(\mathbf{P}_2\) defining the cubic. As you change the curves by dragging the large circles, you should see a small black dot track the intersection point. You will see additional points appear if you orient the curve such that there are multiple intersections. This is shown below in Figure 1.
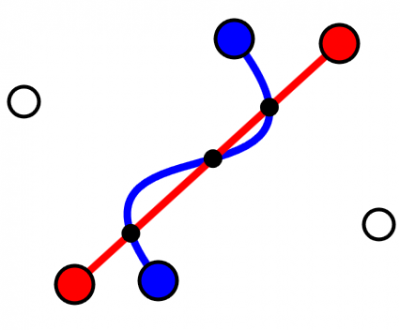
Math Background
So how does this code work? The visualization is similar to the article on smooth splines through prescribed points. This mathematical algorithm is based on this answer. One way to represent an infinitely-long line is as follows
$$\displaystyle \frac{(x-x_1)}{(x_2-x_1)} = \frac{(y-y_1)}{(y_2-y_1)}$$
which can be rewritten as
$$x(y_2-y_1) + y(x_1-x_2) + x_1(y_1-y_2)+y_1(x_2-x_1)=0$$
or
$$ Ax + By + C = 0 \qquad (1)$$
We next constrain the \((x,y)\) pairs to those located on the cubic curve. A cubic Bezier curve is given by
\(\mathbf{r}(t)=(1-t)^3\mathbf{P}_0 + 3(1-t)^2t\mathbf{P}_1 + 3(1-t)t^2\mathbf{P}_2 + t^3\mathbf{P}_3, \quad t\in [0,1]\)
where \(\mathbf{r}(t)\) is the position vector. If we substitute these \((x,y)\) components into equation (1), we obtain a cubic equation in \(t\). Finding the intersection points is then a “simple” matter of finding the roots of the cubic equation.
Cubic Roots
One way to find a single root is using Newton’s method. Unfortunately, a cubic can have up to 3 roots. This is because, as shown in Figure 1, a line can intersect a cubic spline in up to 3 locations. Since we are using this algorithm for particle tracing, we are interested in the first intersection along the line. There is no guarantee that the Newton’s method will converge to this root. As such, we need to find all existing roots and sort them. Finding additional roots with Newton’s method is possible but not trivial. Third-order polynomials also have an analytical solution for their roots. But unlike the well known quadratic formula, there are multiple equations for cubic roots. In the end, I ended up using algorithm from Stephen Schmitt’s site:
/*based on http://mysite.verizon.net/res148h4j/javascript/script_exact_cubic.html#the%20source%20code*/ function cubicRoots(P) { var a=P[0]; var b=P[1]; var c=P[2]; var d=P[3]; var A=b/a; var B=c/a; var C=d/a; var Q, R, D, S, T, Im; var Q = (3*B - Math.pow(A, 2))/9; var R = (9*A*B - 27*C - 2*Math.pow(A, 3))/54; var D = Math.pow(Q, 3) + Math.pow(R, 2); // polynomial discriminant var t=Array(); if (D >= 0) // complex or duplicate roots { var S = sgn(R + Math.sqrt(D))*Math.pow(Math.abs(R + Math.sqrt(D)),(1/3)); var T = sgn(R - Math.sqrt(D))*Math.pow(Math.abs(R - Math.sqrt(D)),(1/3)); t[0] = -A/3 + (S + T); // real root t[1] = -A/3 - (S + T)/2; // real part of complex root t[2] = -A/3 - (S + T)/2; // real part of complex root Im = Math.abs(Math.sqrt(3)*(S - T)/2); // complex part of root pair /*discard complex roots*/ if (Im!=0) { t[1]=-1; t[2]=-1; } } else // distinct real roots { var th = Math.acos(R/Math.sqrt(-Math.pow(Q, 3))); t[0] = 2*Math.sqrt(-Q)*Math.cos(th/3) - A/3; t[1] = 2*Math.sqrt(-Q)*Math.cos((th + 2*Math.PI)/3) - A/3; t[2] = 2*Math.sqrt(-Q)*Math.cos((th + 4*Math.PI)/3) - A/3; Im = 0.0; } /*discard out of spec roots*/ for (var i=0;i<3;i++) if (t[i]<0 || t[i]>1.0) t[i]=-1; /*sort but place -1 at the end*/ t=sortSpecial(t); console.log(t[0]+" "+t[1]+" "+t[2]); return t; }
This algorithm returns an array of parametric intersection locations along the cubic, with -1 indicating an out-of-bounds intersection (before or after the end point or in the imaginary plane). We also need to verify that the intersections are within the limits of the linear segment. This is done by the following code:
/*computes intersection between a cubic spline and a line segment*/ function computeIntersections(px,py,lx,ly) { var X=Array(); var A=ly[1]-ly[0]; //A=y2-y1 var B=lx[0]-lx[1]; //B=x1-x2 var C=lx[0]*(ly[0]-ly[1]) + ly[0]*(lx[1]-lx[0]); //C=x1*(y1-y2)+y1*(x2-x1) var bx = bezierCoeffs(px[0],px[1],px[2],px[3]); var by = bezierCoeffs(py[0],py[1],py[2],py[3]); var P = Array(); P[0] = A*bx[0]+B*by[0]; /*t^3*/ P[1] = A*bx[1]+B*by[1]; /*t^2*/ P[2] = A*bx[2]+B*by[2]; /*t*/ P[3] = A*bx[3]+B*by[3] + C; /*1*/ var r=cubicRoots(P); /*verify the roots are in bounds of the linear segment*/ for (var i=0;i<3;i++) { t=r[i]; X[0]=bx[0]*t*t*t+bx[1]*t*t+bx[2]*t+bx[3]; X[1]=by[0]*t*t*t+by[1]*t*t+by[2]*t+by[3]; /*above is intersection point assuming infinitely long line segment, make sure we are also in bounds of the line*/ var s; if ((lx[1]-lx[0])!=0) /*if not vertical line*/ s=(X[0]-lx[0])/(lx[1]-lx[0]); else s=(X[1]-ly[0])/(ly[1]-ly[0]); /*in bounds?*/ if (t<0 || t>1.0 || s<0 || s>1.0) { X[0]=-100; /*move off screen*/ X[1]=-100; } /*move intersection point*/ I[i].setAttributeNS(null,"cx",X[0]); I[i].setAttributeNS(null,"cy",X[1]); } }
As you can see, we are always plotting 3 intersection locations, but the out-of-bounds intersections are moved off screen to location (-100,-100). The above code also does not sort the intersections along the line, but this change is ease to implement by storing the s parametric positions in array.
Source Code
And that’s it. You can download the code by right clicking and selecting “save as” on this link: cubic-line.svg
Hello,
first I want to say that I really like the blog and topics discussed here. I remember finding the Boris-push post years ago and it helped my a lot at that time.
But on the topic: How do you check if particles are inside your domain? In my problems I just have an arbitrary shaped boundary. I classify each cell as either inside, outside or boundary cell. For the boundary cells I use a (kind of reduced) point-in-polygon check. But how would one do it for cubic splines? Just always calculate if there is an intersection point?
I hope you can clear things up like in the past :).
Cheers
Oli
Hey Oli,
as a quick rejection of collision with bezier, you can check for collision with the hull created by the control points of the bezier. If it doesn’t collide with the hull, it can’t collide with the curve.
from wikipedia:
Bézier curves are widely used in computer graphics to model smooth curves. As the curve is completely contained in the convex hull of its control points, the points can be graphically displayed and used to manipulate the curve intuitively
Hi there,
I guess you may feel interested about my research on curve-to-curve intersection too, https://sites.google.com/site/curvesintersection/
Enjoy my show! Cheers,
Hunt Chang
Thanks for sharing!
Hey! Just wanted to say this was incredibly helpful to me in a project I’m working on. Thanks a lot!
Thanks and glad to hear that!
Your code saved really a lot of time!
Many thanks!!
Thanks for sharing this, it really helped!
It’s good to use generic line equation.
Thanks for the helpful code!
I did find one issue where the calculated coefficients could end up having zero values for either or both of the cube or square with certain configurations (e.g. for A*x^3 + B*x^2 + C*x + D, A and/or B could end up being zero). This causes a divide-by-zero error when attempting to calculate the cubic roots (resulting in the line segment going through the bezier curve but NOT showing an intersection point). I simply added quadratic and linear cases to handle such scenarios.
Here is a scenario that causes the zero coefficients:
/*create control points for the cubic*/ P[0] = createMarkerV(100,50,"blue"); P[1] = createMarkerK(200,250); P[2] = createMarkerK(300,250); P[3] = createMarkerV(400,450,"blue"); /*create control points for the line*/ P[4] = createMarkerV(200,50,"red"); P[5] = createMarkerV(200,350,"red");You can see it happen as you move one of the line segment endpoints around from being vertical to non-vertical.
To fix the issue, I added this to the cubicRoots function:
if( P[0] == 0 ) { if( P[1] == 0 ) { console.log("Linear formula detected"); var t = Array(); t[0] = -1 * ( P[3] / P[2] ); t[1] = -1; t[2] = -1; /*discard out of spec roots*/ for (var i=0;i<1;i++) if (t[i]1.0) t[i]=-1; /*sort but place -1 at the end*/ t=sortSpecial(t); console.log(t[0]); return t; } console.log("Quadratic formula detected"); var DQ = Math.pow(P[2], 2) + 4*P[1]*P[3]; // quadratic discriminant if( DQ >= 0 ) { DQ = Math.sqrt(DQ); var t = Array(); t[0] = -1 * ( ( DQ + P[2] ) / ( 2 * P[1] ) ); t[1] = ( ( DQ - P[2] ) / ( 2 * P[1] ) ); t[2] = -1; /*discard out of spec roots*/ for (var i=0;i<2;i++) if (t[i]1.0) t[i]=-1; /*sort but place -1 at the end*/ t=sortSpecial(t); console.log(t[0]+" "+t[1]); return t; } }Again, awesome code!
Hey man, thank a lot for this improvement ! But I found a syntax error. Here is the final code I think :
function cubicRoots(P)
{
if( P[0] == 0 )
{
if( P[1] == 0 )
{
console.log(“Linear formula detected”);
var t = Array();
t[0] = -1 * ( P[3] / P[2] );
t[1] = -1;
t[2] = -1;
/*discard out of spec roots*/
for (var i=0;i<1;i++)
if (t[i]1.0) t[i]=-1;
/*sort but place -1 at the end*/
t=sortSpecial(t);
console.log(t[0]);
return t;
}
console.log(“Quadratic formula detected”);
var DQ = Math.pow(P[2], 2) – 4*P[1]*P[3]; // quadratic discriminant
if( DQ >= 0 )
{
DQ = Math.sqrt(DQ);
var t = Array();
t[0] = -1 * ( ( DQ + P[2] ) / ( 2 * P[1] ) );
t[1] = ( ( DQ – P[2] ) / ( 2 * P[1] ) );
t[2] = -1;
/*discard out of spec roots*/
for (var i=0;i<2;i++)
if (t[i]1.0) t[i]=-1;
/*sort but place -1 at the end*/
t=sortSpecial(t);
console.log(t[0]+” “+t[1]);
return t;
}
}
well…
I understand now why there was an syntax error. This appear when we copy past in this comment section the code near “/*discard out of spec roots*/”
You just need to copy the original post for this part, don’t copy past the code I sent.
Should be: if (t[i]<0 || t[i]>1.0) t[i]=-1;
When typing the symbols for less-than (<) and greater-than (>), the browser will first try to interpret them as HTML tags. Only when it fails to do so will it display them as symbols.
Thanks!
By the way,
should have been
I accidentally used a ‘+’ in the place of a ‘-‘.
Thank u a lot.it’s interesting.
This is a GREAT demo. Any updates to this? It is very useful sample. I’m working with it trying to make it work for multiple lines but still allowing for multiple intersections per line, and I have also run into the issue Joshua ran into. If you have any updates or info to share that would be very appreciated.
I wasn’t really planning on making any updates to this, but I guess I should implement Joshua’s fixes. One of these days. I can help you with your code offline (email me directly) if needed. Truly, I am quite surprised by how much interest this article generated. This is really an off-shoot of my main work (plasma modeling) but it seems this is the most interesting article on the entire blog!
That’s definitely because bezier curves are more widespread than plasma modeling
Hi,
Thanx for your code, it works perfectly.
However, it seems I cannot find the explanation for that part of code:
var P = Array(); P[0] = A*bx[0]+B*by[0]; /*t^3*/ P[1] = A*bx[1]+B*by[1]; /*t^2*/ P[2] = A*bx[2]+B*by[2]; /*t*/ P[3] = A*bx[3]+B*by[3] + C; /*1*/What does it do, what math is behind it?
It looks like this is the key to the whole thing of plugging two equations together and it’s not explained or I could not comprehend it.
Regards, Sergiy
Hi Sergiy,
I probably should have included more of the intermediate math. Basically, we have the equation Ax+By+C=0. We can however rewrite both x and y as functions of t. This will then give you A*x(t) + B*y(t) + C = 0, which is now an equation in only a single unknown (t) that we can find root(s) for. A Bezier curve can be converted to form x = bx[0]*t^3 + bx[1]*t^2 + bx[2]*t + bx[3] (ignore the coefficient ordering, in hindsight they should be numbered in reverse). Similar equation exists for y. You can plug these into the A*x(t) + B*y(t) + C = 0 equation. You will then obtain the following equation (A*bx[0]+B*by[0])*t^3 + (A*bx[1]+B*by[1])*t^2 + (A*bx[2]+B*by[2])*t + (A*bx[3]+B*by[3]+C) = 0, or P0*t^3 + P1*t^2 + P2*t + P3 = 0.
Hello, thank’s a lot, this was very helpful for a project !!!!
Thanks for this – very useful! I was able to translate this into NodeBox 3 (a visual language).
One problem. I found erratic behavior in some cases which turned out to be rounding errors when some of the intermediate values became extremely large or small. This happened in some cases when control point values had repeating decimals (e.g. 133.3333333333)
I was able to solve this by rounding the X and Y values of the initial four bezier points to two digits of precision (e.g. 133.33333333333 becomes 133.33). This made no visible impact on the lines, curves, or intersection points and solved the problem.
Hi! How would I use this method in a C++ program?
I am a little lost on the function bezierCoeffs.
What does it really doing? Just transferring given coordinates into an array of bx?
I mean is bx[0] = px[0]; bx[1] = px[1]…? or is there any calculation within that function?
var bx = bezierCoeffs(px[0],px[1],px[2],px[3]);
var by = bezierCoeffs(py[0],py[1],py[2],py[3]);
var P = Array();
P[0] = A*bx[0]+B*by[0]; /*t^3*/
P[1] = A*bx[1]+B*by[1]; /*t^2*/
P[2] = A*bx[2]+B*by[2]; /*t*/
P[3] = A*bx[3]+B*by[3] + C; /*1*/
Answering myself.
Looking at the source code, answer is pretty simple.
I can even understand the name of the function now 🙂
function bezierCoeffs(P0,P1,P2,P3)
{
var Z = Array();
Z[0] = -P0 + 3*P1 + -3*P2 + P3;
Z[1] = 3*P0 – 6*P1 + 3*P2;
Z[2] = -3*P0 + 3*P1;
Z[3] = P0;
return Z;
}