On partial pressure determination of condensable materials with a TQCM

Introduction

Last week I attended the 49th AIAA Joint Propulsion Conference in San Jose, CA. The conference was a bit slim on EP papers, which is probably due to the upcoming IEPC at GWU this October. But I got to see an interesting paper on facility pressures. The paper, AIAA-2013-4129, was by Mark A. Hopkins and Lyon B. King from the Michigan State University, and was titled “Evaluation of a Plasma Impedance Probe in a Time-varying Non-uniform Plasma”. In the paper the authors discussed difficulties in utilizing conventional pressure gauges for determining vacuum chamber background pressure when testing a magnesium Hall thruster. The authors attempted to use a method based on antenna impedence but it was not completely successful due noise associated with temporal and spatial non-uniformities. The purpose of this post is to derive an alternative approach based on utilizing a quartz crystal microbalance (QCM). The post also includes an interactive demo you will find below.

Background Info

First as a bit of background, most Hall thrusters operate on gaseous propellants such as xenon or argon. However, number of researches have demonstrated feasibility of utilizing non-gaseous propellants with bismuth being a popular option. These solid or liquid propellants have the advantage of not requiring the high pressure tanks associated with the traditional systems. However, the major drawback is that, due to the fact that these propellants are solid or liquid at room temperature, the plume will end up condensing on pretty much anything it comes in contact with. Running a bismuth or a magnesium thruster is a great way to coat your vacuum chamber and any GSE with a thin metallic layer. Of course, this is a huge contamination concern for a spacecraft integration that will need to be resolved before there is any chance of flying such Hall thrusters on an actual mission.

I wasn’t aware of this, but turns out that one of the difficulties in testing these non-traditional Hall thrusters is in determining the chamber operating pressure. Vacuum chambers do not actually achieve vacuum – instead the pressure in the chambers is driven by the pumping speed and the rate at which gas sources such as molecular outgassing, gas leaks, and actual gas injections are introduced into the chamber. Typical operating pressures for a large chamber is around 5×10^-6 Torr. Since atmospheric pressure is 760 Torr, this is about one billionth of the ambient pressure. Although this seems like a rather tiny fraction, we can see that in fact it is not. Using the ideal gas law \(P=nkT\), we can estimate the background number density in a chamber pumped to 5×10^-6 Torr at ambient temperature to be 1.6×10¹⁷ m^-3. This is the same order of magnitude as the near plume ion density of a typical Hall thruster and about 10% of the near plume neutral density. Number of papers [1-2] have been written on the effect of facility background pressure on the operation of Hall effect thrusters. In order to correlate the thruster performance data captured in a vacuum chamber to the on-orbit environment, we need to know the facility pressure.

Chamber Instrumentation

Ion Gauges

Typically, pressure in a vacuum chamber is measured with an ionization gauge or ion gauge for short. Several different companies manufacture these devices, including Lesker and Brooks Granville Phillips. Besides the old-fashioned glass type, modern ion gauges also come in more compact metal casings, such as the Granville Phillips Series 355. Regardless of packaging, they all operate on the same principle. The gauge uses a hot filament to emit electrons which in turn ionize the local environment. The filament is located outside a spiral-type anode which is biased positive in respect to the emitter. This anode screens out the electrons. Only ions can get inside where they are collected by a rod-like cathode. The collected current is used to calculte the chamber pressure by assuming a certain ionization cross-section based on the expected dominant gas in the chamber. These gauges are susceptible to contamination. Molecular contaminants can deposit on the filament and reduce the emission current. They can also interfere with the current collection at the collector. Even in a clean vacuum environment, ion gauges need to be regularly heated to bake off the deposited contaminants. Based on a comment of the paper authors, ion gauges cannot handle the contamination from the condensable magnesium propellant. As such, during the thruster tests, it becomes impossible to determine the chamber pressure. This is what led the authors to investigate alternative methods.

Quartz Crystal Microbalance (QCM)

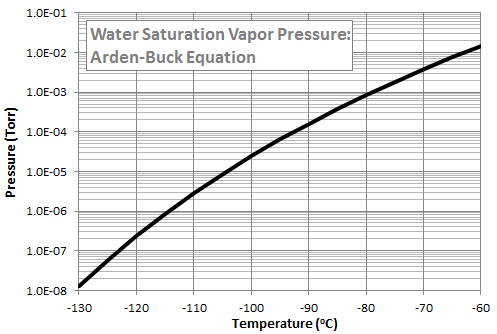
While listening to the talk, I started thinking that perhaps a QCM could be a viable alternative. QCM, or quartz crystal microbalance, is a diagnostic tool for determining the amount of mass condensing on a surface. QCMs are used in the spacecraft industry during bakeouts of space hardware to determine the amount of molecular outgassing. They have also been used to determine differential sputter yield of materials [3]. A QCM contains two small crystals. One is exposed to the ambient environment and the other one is sealed for reference. QCMs come in one of three variants: passive, cryogenic, and thermoelectric. As mass deposits on the exposed crystal, the crystal vibrational frequency increases, and from this frequency increase, we can calculate the amount of deposited mass. The difference between the QCM types is their ability (or lack off) to maintain a certain crystal temperature. A Thermoelectric QCM (TQCM) contains an internal heater and a Peltier cooler to actively maintain the crystal temperature at a preset level. A popular TQCM is Mark 10 by QCM Research. The Peltier element is capable of lowering the temperature to some 40^oC below the TQCM head temperature. The reason this is important is that different chemical species have different condensation temperatures. As an example, Figure 2 plots the saturation vapor pressure of water computed using the Arden Buck equation. We see that we would need to cool the QCM crystal to well below -100^oC in order to condense water in the typical vacuum chamber environment. The TQCM thus gives us the ability to tune the collection to materials of interest such as hydrocarbons condensing at or above sensitive surface temperatures while ignoring benign species like water.

This brings us back to the paper. The authors mentioned they in fact had tried using a QCM but their difficulty was that they could not control the temperature. This makes me suspect their setups utilized a passive QCM instead of a TQCM. Assuming this simple fix is done, my suggestion for the process is as follows:

1. Load the chamber with the thruster and all GSE that will be used for testing. Use an ion gauge to determine the baseline pressure which will include contribution from all non-magnesium sources.
2. Determine baseline collection rate of the TQCM set to a high enough temperature to prevent deposition of majority of hydrocarbons while still allowing the Magnesium to condense. This should be close to zero.
3. Use the TQCM to determine the partial pressure of magnesium. Add this partial pressure to the baseline pressure to determine total pressure.
4. Periodically bake-off the deposited magnesium off the QCM crystal (this may be a challenge)

One difficulty here is that unlike regular gas molecules that bounce around the chamber until they find a cold surface (i.e. the pump), magnesium is expected to stick on the first impact. As such, the pressure measurement will be very localized. We also cannot measure in the expected high-pressure regions since this would rapidly saturate the crystal. The off-centerline pressure will be driven by charge exchange transport and also by diffusion of the non-ionized propellant. It will not influenced by wall scattering which, in the case of free-molecular flow, is the primary transport mechanism. As such, it will likely be necessary to utilize several QCMs to determine local pressures in multiple locations and combine the experimental effort with numerical simulations to obtain a map of internal pressure distribution.

Langmuir Flux

But how can we determine gas pressure from the QCM collection rate? Kinetic theory gives us a relationship between pressure and surface flux, Langmuir flux. This expression tells us that
$$\Gamma = \dfrac{n\bar{u}}{4}$$
where the mean velocity assuming the Maxwellian distribution is
$$\bar{u} = \sqrt{\dfrac{8kT}{\pi m}}$$
and the number density can be related to pressure via the ideal gas law
$$p=nkT$$

Hence, if we assume Maxwellian distribution and know the mass and temperature of the condensing material, we can compute the volumetric pressure from knowing the local surface flux. Using data for the QCM Research Mark 10 TQCM with the 15MHz crystal, the mass sensitivity is 5.09×10⁸ (Hz/g) cm². Hence, an increase of 1Hz in crystal frequency corresponds to surface flux of
$$\Delta f \left(1 \text{Hz}\right) \to \dfrac{1}{5.09\times 10^8} \dfrac{\text{g}}{\text{cm}^2}$$
Assuming atomic magnesium with mass of 24.3 amu, to frequency change rate can be correlated to number flux as
$$\Delta r \left(1 \text{Hz/s}\right) \to 4.87\times 10^{17} \text{m}^{-2}/\text{s} \quad \text{Mg}$$

Interactive Demo

Above is all the math we need estimate pressure from surface flux. However, I wanted to make sure this indeed worked, so I put together a simple collisionless simulation which you can run in your browser by pressing the green “GO” button. This simulation utilizes techniques described previously in an article on using HTML5 for scientific computing. It starts off by loading gas at 300K and 5×10^-6 Torr using the method on loading an isotropic Maxwellian velocity distribution. The atoms bounce around (the code also implements periodic boundaries which you can switch on in the source code) except that those atoms reaching the simulation QCM in the bottom right corner are counted and absorbed. From this simple count of absorbed molecules, the code calculates the gas pressure. You will see that it is indeed close to the expected value.

Numerical Cooling

As a final note, if you look through the code you will notice that it computes the pressure as

/*calculations*/
var ave=count/(it*dt);
var flux=spwt*ave/100;  /*100 is the qcm length * unit depth*/
var uc = usum/np;   /*average velocity from simulation, u_ave is kinetic theory*/
var den=flux*4/uc;  /*using uc instead of u_ave due to numerical cooling*/
var P=den*k*T/133.32;

where uc is the average velocity computed from the actual gas molecules instead of utilizing the average velocity from kinetic theory mentioned above. This is because this code suffers from numerical cooling. In the simulation we use only 150 particles to represent the Maxwellian speed distribution. Whenever a particle hits the QCM, we sample a new particle. Now, since faster particles have a higher chance of hitting the QCM, they will be depleted faster. However, when we load a new particle, there is a higher probability of loading a particle closer to the mean velocity. This then shifts the distribution function which is analogous to reduction in temperature. You can in fact watch this decrease in the results box.