Get results faster with Java multithreading

Code Parallelization
Code parallelization is the process of modifying a simulation code to make it run faster by splitting the workload among multiple computers (well, in the very general sense). There are many options available. MPI is a widely used networked protocol that allows programs running on different computers to communicate with each other. It is deigned for use on clusters, arrays of hundreds and even thousands of individual computers linked together by network cables. OpenMP uses a different model. It is a set of compiler constructs that allow incorporation of multithreading into C and Fortran codes. As such, it is suitable for fine-grade parallelization on machines containing multiple cores sharing the same memory (such as most modern PCs). A relative newcomer to the game is Cuda. Cuda is a special interface language that allows you to write code that runs not on the CPU, but on a compatible NVIDIA GPU (graphics card). GPUs are basically highly optimized vector computers. They can execute single instruction on multiple data concurrently. In the world of particle plasma simulations, this means you can for instance push hundreds of particles at the same time.
Multithreading
These three methods allow you to write your program in a specific way so that it can run faster. Usually the serial (single processor) version is written first, and after it is shown to work for a smaller domain set, the program is parallelized, and eventually used to run simulation on a large domain. Parallelization of a serial code is a nontrivial task. It requires significant code changes and time devoted to debugging. However, sometimes parallelization is not actually necessary. Often, we need to run a single program multiple times to analyze the dependence of results on some input parameter. Instead of making each case execute faster, we can obtain the final set in shorter time by simply running the multiple cases concurrently. If the number of cases is small, this can be done by simply building several versions of the executable and launching them individually. However, if the number of required cases is larger than the number of CPUs, such an approach will result in non-optimal performance. Often, we are also interested in doing some post-processing of the data – each simulation may correspond to just a single point on an XY plot. We prefer for the main program to parse these, and output a single file containing results from all the simulations.
We can hence utilize multithreading by launching each case as a separate thread. A simple scheduler will make sure than only as many threads are running at one time as there are CPU cores. And while OpenMP is required to add multithreading into C codes, Java supports multithreading natively. If your code already happens to be written in Java, it becomes very simple to add multithreading support.
It should be noted that true parallelization offers some benefits over the simple method presented here. For instance, by distributing the problem to multiple CPUs we can simulate domains larger than could fit in the memory of a single machine. The method presented here results in each case running serially and hence memory constraints still apply. This method is best suited for codes that do not require large amounts of memory, and also take comparable computational times for the inputs tested.
Example
We will demonstrate this method using a simple example: computing pi.The task at hand is: compute pi by sampling some specified number of points and compute the error. Simple way to calculate pi is to pick random points in [0,1]x[0,1] domain. Next imagine that a circle of radius 1 is drawn at the origin. One quarter of the circle will be located in this 1×1 domain. The ratio of points lying inside the circle to the total number of points is directly related to the ratio of the area of the quartercicle to the square. In other words, [latex]displaystyle n_c=frac{pi}{4}n_0[/latex]. We can determine if the point is inside or outside the circle from sqrt(x*x+y*y)<1. Due to the statistical number of computations, the computed error will vary from run to run. To get a more accurate result, we need to repeat the simulation multiple times and average the result. The code below illustrates how this task would be handled serially. The main function consists of a loop that executes the simulation 24 times. After each simulation finishes, the code adds the resulting error to a running sum. Once the loop completes, the average error is shown on the screen. Of course, your program would do something more useful than calculate pi. For instance, the calls to calculatePI() could be calls to execute the main loop in a particle in cell plasma simulation for a different range of input plasma parameters…
/*------ Main.java -----------*/public class Main
{public static void main(String[] args)
{double sum = 0;
int ns=24; /*number of computations*/
/*sample 50,000 x 1,000 points*/Simulation sim = new Simulation(50000);
for (int i=0;i<ns;i++)
{sim.computePI();
sum += sim.getError();
}System.out.printf("Average error is %gn", sum/ns);
}}/*------ Simulation.java -----------*/public class Simulation
{protected double result; /*result*/
protected double error; /*error in percent*/
protected int nk;
double getResult() {return result;}
double getError() {return error;}
Simulation (int nk)
{this.nk = nk;
}/*CalculatesPI by taking nk*1000 sample points*/void computePI()
{double x,y;
double r;
int i,j=0;
int count=0;
for (i=0;i<nk;i++)
for (j=0;j<1000;j++)
{/*select random point*/x = Math.random();
y = Math.random();
r=Math.sqrt(x*x+y*y);
if (r<=1.0)
count++;}result = 4*count/(double)(nk*j);
error = 100*Math.abs(result-Math.PI)/Math.PI;
System.out.printf(" nk = %d:t pi = %g,t error = %.2g%%n", nk,result,error);
}}
Parallel version
Our goal is to execute each computation as an individual thread. This requires few small changes to our class Simulation. First, the class needs to extend the base class Thread. The class must implement a routine public void run(), which will be executed when the thread is started by calling start(). This routine then in turns executes the computation. Finally we modify the constructor to take in few extra parameters: name and ThreadGroup. These are passed over to the base class. Java lets you define multiple thread groups to better organize the computation. The name argument can be used to uniquely identify the thread. Although we give each thread a unique name, this is not necessary. The name is also not being used by our example.
/*------ Simulation.java -----------*/class Simulation extends Thread
{protected double result; /*result*/
protected double error; /*error in percent*/
protected int nk;
double getResult() {return result;}
double getError() {return error;}
Simulation (int nk, String name, ThreadGroup tg)
{super(tg,name);
this.nk = nk;
}public void run()
{computePI();
}/*CalculatesPI by taking nk*1000 sample points*/void computePI()
{/* same code as above */}}
We next need to modify the main loop. Since the simulations run concurrently, we need to instantiate each case as a new instance. The instances are stored in an array list. We create only one thread group, and associate each instance with it. We also determine how many processors Java has access to. We next incorporate a simple scheduler. The scheduler checks if the number of currently active threads is less than the number of available cores. If so, it launches another simulation from the list of cases to run. Otherwise if there are no free cores, it goes to sleep for 0.1 seconds. This sleep command is necessary to prevent overloading the CPU with calls to activeCount. The loop continues until all cases have been launched. After this, we wait for all simulations to finish running using a similar logic. We then loop through all our instances and calculate the running sum. The sum is outputted, along with the simulation time.
/*------ Main.java -----------*/import java.util.*;
public class Main
{public static void main(String[] args)
{ThreadGroup tg = new ThreadGroup("main");
int np = Runtime.getRuntime().availableProcessors();
int i, ns=24;
List<Simulation> sims = new ArrayList<Simulation>();
long start = System.nanoTime();
for (i=0;i<ns;i++)
sims.add(new Simulation(50000,"PI"+i, tg));
i=0;
while (i<sims.size())
{/*do we have available CPUs?*/if (tg.activeCount()<np)
{Simulation sim = sims.get(i);
sim.start();
i++;} else
try {Thread.sleep(100);} /*wait 0.1 second before checking again*/
catch (InterruptedException e) {e.printStackTrace();}
}/*wait for threads to finish*/while(tg.activeCount()>0)
{try {Thread.sleep(100);}
catch (InterruptedException e) {e.printStackTrace();}
}/*sum up errors*/double sum=0;
for (i=0;i<sims.size();i++)
{Simulation sim = sims.get(i);
sum+=sim.getError();
}long end = System.nanoTime();
System.out.printf("Average error is %gn", sum/sims.size());
System.out.printf("Simulation took %.2g secondsn", (double)(end-start)/1e9);
}}
Performance checking
That’s it, or is it? Whenever parallelizing code, you should always include benchmarking to make sure that the parallelized version indeed works as expected. Case in point. The serial version takes 75 seconds to complete on my machine. The version utilizing 8 CPU cores takes 250 seconds! And this is despite the Windows Task Manager showing 100% utilization of the CPUs. Not only did increasing the machine power by a factor of 8 not speed up the code, it in fact slowed it down by over 3 times. What’s going on?
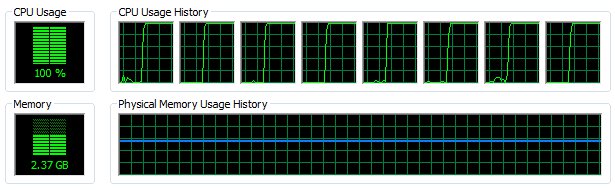 Java documentation states “This method is properly synchronized to allow correct use by more than one thread. However, if many threads need to generate pseudorandom numbers at a great rate, it may reduce contention for each thread to have its own pseudorandom-number generator.” In other words, the built-in random function is designed such that only one tread can access it at a time. Despite launching multiple threads, only one is actually executing at any given time. The others are waiting for the other thread to return from the call to random. To correct this issue, we need each thread to create it’s own instance of the random number generator, Random rnd = new java.util.Random();. We then sample random numbers using rnd.nextDouble();. The updated code is shown below.
Java documentation states “This method is properly synchronized to allow correct use by more than one thread. However, if many threads need to generate pseudorandom numbers at a great rate, it may reduce contention for each thread to have its own pseudorandom-number generator.” In other words, the built-in random function is designed such that only one tread can access it at a time. Despite launching multiple threads, only one is actually executing at any given time. The others are waiting for the other thread to return from the call to random. To correct this issue, we need each thread to create it’s own instance of the random number generator, Random rnd = new java.util.Random();. We then sample random numbers using rnd.nextDouble();. The updated code is shown below.
/*------ Simulation.java -----------*/import java.util.Random;
public class Simulation extends Thread
{protected double result; /*result*/
protected double error; /*error in percent*/
protected int nk;
Random rnd;
double getResult() {return result;}
double getError() {return error;}
Simulation (int nk, String name, ThreadGroup tg)
{super(tg,name);
this.nk = nk;
rnd = new java.util.Random();
}public void run()
{computePI();
}/*CalculatesPI by taking nk*1000 sample points*/void computePI()
{double x,y;
double r;
int i,j=0;
int count=0;
for (i=0;i<nk;i++)
for (j=0;j<1000;j++)
{/*select random point*/x = rnd.nextDouble();
y = rnd.nextDouble();
r=Math.sqrt(x*x+y*y);
if (r<=1.0)
count++;}result = 4*count/(double)(nk*j);
error = 100*Math.abs(result-Math.PI)/Math.PI;
System.out.printf(" nk = %d:t pi = %g,t error = %.2g%%n", nk,result,error);
}}
This change reduced the computational time on 8 cores from 250 seconds to 16. Quite impressive! It also means that the serial version that took 75 seconds was sped up by a factor of 4.7 by employing 8 cores. This is a far stretch from the expected 8x speed up, however ratios like these are much more realistic. And that’s it. Feel free to leave a comment if you have any questions or if something isn’t clear.
Lubos,
I just read the article on Java Multithreading. You did a real good job with this one. It is very easy to understand.
Here is the Java Multithreading example implemented as an applet in a webpage.
http://dl.dropbox.com/u/5095342/PIC/JavaMT/JavaMT.html
It also makes use of the livescript capabilities to communicate between Java in the applet and Javascript in the webpage.
http://jdk6.java.net/plugin2/liveconnect/
Hi!
Firstly, I want to congratulate your good work and explanation of multithreading in Java.
I’m doing a parallel version of a algorithm and I have the same problem! I removed the synchronized methods implemented by me, but, I think there are something that slowdown my parallel application.
Can you tell me another tips that can slowdown the speed of my application?
Thank you very much!
Henrique
________________________
University Technologic Federal of Parana
Brazil
Enginnering Computing
Hi Henrique, it’s kind of hard to answer your question without seeing the details of your code. Not sure what development environment you use, but NetBeans includes a profiler you can use to check the speed of your code which could give you some hints.
Hi Lubos,
I’m using NetBeans.
To test my application I use the NetBeans profiler. But, I only see the CPU/MEM usage.
I tracked the function with more CPU usage and I found the “heavy function”.
I parallelized this function and, I have the same result that you got. My 4 cores are in 100% of load of each core. But, I get the same time of sequential code! (like your first situation)
After, I removed the synchronous functions and static methods, but the time continue poor!
Can you tell me if NetBeans profiler has a feature that I can use to track it? If you can contact by e-mail, please, ok?
Thanks!
Henrique,
See if this helps: http://forums.netbeans.org/topic25037.html
You may also want to investigate
http://docs.oracle.com/javase/6/docs/api/java/lang/management/ThreadMXBean.html. This class can be used to obtain useful information about threads, see http://stackoverflow.com/questions/217113/deadlock-in-java
Very nice! Right to the point!
When I tested the first parallel version, I thought: this is much slower. hehe xD
I want to get high speed performance for my mathematical computation.So,I will use Thread in java.But when I run the simple code about thread in java from google,the execution time is more longer than the simple program.How I can solve it?
Help me.
Thanks
If you’re every scholar looking to spend much less on the protection,
have a take a look at citizen school student discounts https://math-problem-solver.com/ .
The top rated ( ) often signifies that the side
is in the route of be up-to-date via the really worth upon the particularly.
I recommend not using java.util.Random over ThreadLocalRandom, not only is ThreadLocalRandom more readable, it is also perfect for this scenario: random numbers in parallel in thread pools (as stated by the javadocs), this also has much less overhead.
Thanks Ryan! I am not even familiar with this class. It may not have even existed when this article was written (using Java 6 I believe).