Flow in a Nozzle

This semester I am teaching MAE6229, Propulsion, at the George Washington University. By considering one-dimensional flow, one can derive the following relationship for the Mach number,
$$\frac{dM^2}{dx}=\frac{M^2\left[1+\frac{\gamma-1}{2}M^2\right]}{1-M^2}\left[-\frac{2}{A}\frac{dA}{dx} +\left(1+\gamma M^2\right)\frac{1}{T_0}\left(\frac{dT_0}{dx}\right) +4\gamma M^2 \frac{C_f}{D} \right]$$
where the terms on the right correspond to area change, heat addition, and friction, respectively. This is Equation 3.29 in Hill and Peterson. This equation is in general too complex to solve analytically, but we can use numerical techniques. One approach is to use the forward difference, and integrate the Mach number as
$$\displaystyle M (x+\Delta x)=M(x)+\sqrt{\frac{dM^2}{dx}(x)\Delta x}$$.
What’s interesting about the above equation, is that we can see that we can get a continuous solution only if the last term (containing the area, temperature, and friction contributions) disappears as \(M\to 1\). For instance, let’s consider the simplified case of flow in a duct with area change, but without heat addition or friction. The equation then simplifies to
$$\displaystyle \frac{dM^2}{dx}=M^2\left[1+\frac{\gamma-1}{2}M^2\right]\frac{\left[-\dfrac{2}{A}\dfrac{dA}{dx} \right]}{1-M^2}$$
Since we require the right hand side to be positive (since \(dM^2\) on the left hand side), we can see we can get a real solution only if
$$ \dfrac{dA}{dx}<0 \qquad :M<1$$ and $$ \dfrac{dA}{dx}>0 \qquad :M>1$$
Exactly at \(M=1\), we require \(\dfrac{dA}{dx}=0\)

In other words, if the flow is initially subsonic, it needs to first pass through a converging duct in order to accelerate. Exactly at $latex M=1$, there needs to be an inflection point, after which the duct must start diverging to accelerate it to the supersonic speeds. This is the basis behind the converging-diverging nozzle used in chemical rockets.

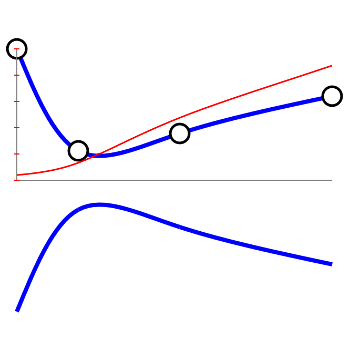
Interactive Demo

The above equation (for the case of area change without heat or friction) is implemented below. You can drag the top 4 circles to change the shape of the nozzle. I am using a simple algorithm to set the flow to \(M>1\) if \(dM^2/dx<0\), which will show up as a step function if the flow is not matched properly. But you will see that if you rearrange the shape of the nozzle, you will be able to get a flow that accelerates smoothly from \(M=0.1\) at the inlet, through \(M=1\) in the throat, to $latex M>1$ in the diverging section. One such solution is plotted below in Figure 1.