2D Finite Element Method in MATLAB

This guest article was submitted by John Coady (bio below). Would you like to submit an article? If so, please see the submission guidelines. If your article is on scientific computing, plasma modeling, or basic plasma / rarefied gas research, we are interested! You may also be interested in an article on FEM PIC.
Finite Element Method in Matlab
The Finite Element Method is one of the techniques used for approximating solutions to Laplace or Poisson equations. Searching the web I came across these two implementations of the Finite Element Method written in less than 50 lines of MATLAB code:
The first one of these came with a paper explaining how it worked and the second one was from section 3.6 of the book “Computational Science and Engineering” by Prof. Strang at MIT. I will use the second implementation of the Finite Element Method as a starting point and show how it can be combined with a Mesh Generator to solve Laplace and Poisson equations in 2D on an arbitrary shape. The MATLAB code in femcode.m solves Poisson’s equation on a square shape with a mesh made up of right triangles and a value of zero on the boundary. Running the code in MATLAB produced the following
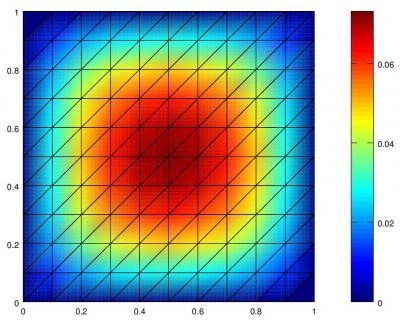
If you look at the Matlab code you will see that it is broken down into the following steps.
- First it generates a triangular mesh over the region
- Next it assembles the K matrix and F vector for Poisson’s equation KU=F from each of the triangle elements using a piecewise linear finite element algorithm
- After that it sets the Dirichlet boundary conditions to zero
- It then solves Poisson’s equation using the Matlab command U = KF
- Finally it plots the results
This particular problem could also have been solved using the Finite Difference Method because of it’s square shape. One of the advantages that the Finite Element Method (and the Finite Volume Method) has over Finite Difference Method is that it can be used to solve Laplace or Poisson over an arbitrary shape including shapes with curved boundaries.
Solving 2D Poisson on Unit Circle with Finite Elements
To show this we will next use the Finite Element Method to solve the following poisson equation over the unit circle, \(-U_{xx} -U_{yy} =4\), where \( U_{xx}\) is the second x derivative and \( U_{yy}\) is the second y derivative. This has known solution
\(U=1-x^2 -y^2\) which can be verified by plugging this value of U into the equation above giving the result 4 = 4 . Although we know the solution we will still use the Finite Element Method to solve this problem and compare the result to the known solution.The first thing that Finite Elements requires is a mesh for the 2D region bounded by the arbitrary 2D shape. In order to do this we will be using a mesh generation tool implemented in MATLAB called distmesh. You can find out more about the distmesh tool and how to use it here. We will use distmesh to generate the following mesh on the unit circle in MATLAB.
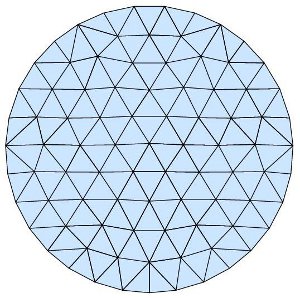
We created this mesh using the following distmesh commands in MATLAB.
fd=@(p) sqrt(sum(p.^2,2)) -1; [p,t] = distmesh2d(fd,@huniform,0.2,[-1,-1;1,1],[]);
The values [p,t] returned from the distmesh2d command contain the coordinates of each of the nodes in the mesh and the list of nodes for each triangle. Distmesh also has a command for generating a list of boundary points b from [p,t],
e = boundedges(p,t); b = unique(e);
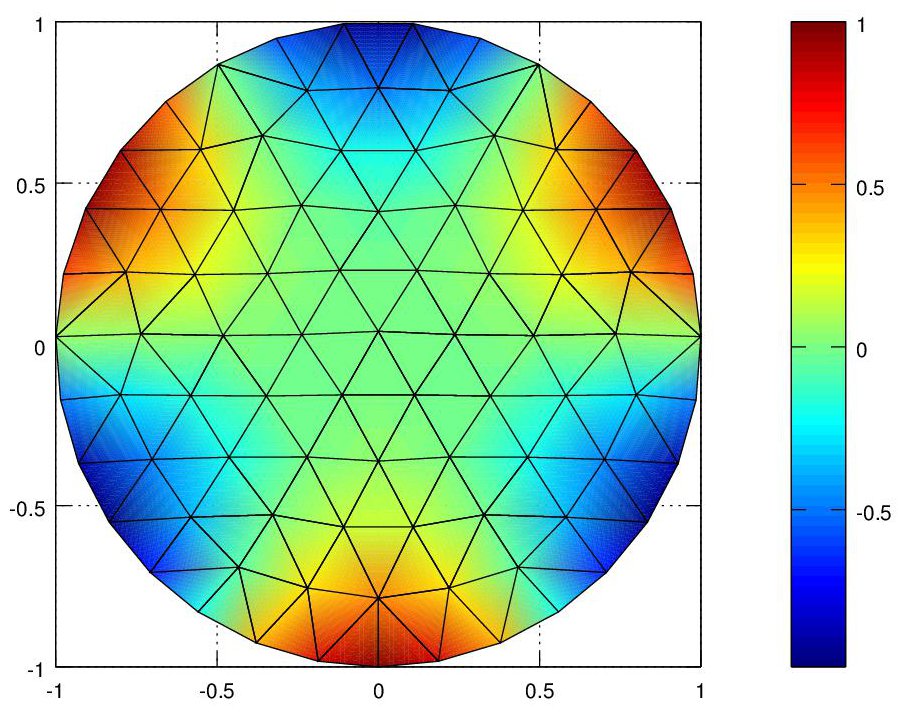
The Finite Element method from the first example requires p, t and b as inputs. We will now modify this first example and to use p, t and b generated by distmesh for the region bounded by the unit circle. This can be accomplished by replacing the mesh generation code from the first part of femcode.m with the mesh creation commands from distmesh. The modified code is shown below and produced the result in Figure 3.
% femcode2.m % [p,t,b] from distmesh tool % make sure your matlab path includes the directory where distmesh is installed. fd=@(p) sqrt(sum(p.^2,2))-1; [p,t]=distmesh2d(fd,@huniform,0.2,[-1,-1;1,1],[]); b=unique(boundedges(p,t)); % [K,F] = assemble(p,t) % K and F for any mesh of triangles: linear phi's N=size(p,1);T=size(t,1); % number of nodes, number of triangles % p lists x,y coordinates of N nodes, t lists triangles by 3 node numbers K=sparse(N,N); % zero matrix in sparse format: zeros(N) would be "dense" F=zeros(N,1); % load vector F to hold integrals of phi's times load f(x,y) for e=1:T % integration over one triangular element at a time nodes=t(e,:); % row of t = node numbers of the 3 corners of triangle e Pe=[ones(3,1),p(nodes,:)]; % 3 by 3 matrix with rows=[1 xcorner ycorner] Area=abs(det(Pe))/2; % area of triangle e = half of parallelogram area C=inv(Pe); % columns of C are coeffs in a+bx+cy to give phi=1,0,0 at nodes % now compute 3 by 3 Ke and 3 by 1 Fe for element e grad=C(2:3,:);Ke=Area*grad'*grad; % element matrix from slopes b,c in grad Fe=Area/3*4; % integral of phi over triangle is volume of pyramid: f(x,y)=4 % multiply Fe by f at centroid for load f(x,y): one-point quadrature! % centroid would be mean(p(nodes,:)) = average of 3 node coordinates K(nodes,nodes)=K(nodes,nodes)+Ke; % add Ke to 9 entries of global K F(nodes)=F(nodes)+Fe; % add Fe to 3 components of load vector F end % all T element matrices and vectors now assembled into K and F % [Kb,Fb] = dirichlet(K,F,b) % assembled K was singular! K*ones(N,1)=0 % Implement Dirichlet boundary conditions U(b)=0 at nodes in list b K(b,:)=0; K(:,b)=0; F(b)=0; % put zeros in boundary rows/columns of K and F K(b,b)=speye(length(b),length(b)); % put I into boundary submatrix of K Kb=K; Fb=F; % Stiffness matrix Kb (sparse format) and load vector Fb % Solving for the vector U will produce U(b)=0 at boundary nodes U=KbFb; % The FEM approximation is U_1 phi_1 + ... + U_N phi_N % Plot the FEM approximation U(x,y) with values U_1 to U_N at the nodes trisurf(t,p(:,1),p(:,2),0*p(:,1),U,'edgecolor','k','facecolor','interp'); view(2),axis([-1 1 -1 1]),axis equal,colorbar
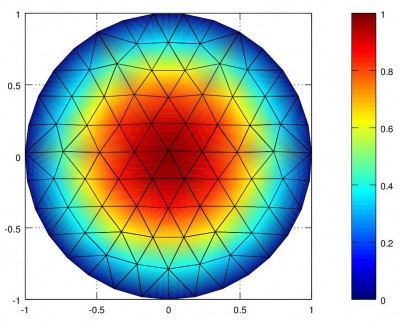
We can compare this result to the known solution \(u = 1 – x^2 – y^2\) to our poisson equation which is plotted below for comparison. We generated this plot with the following MATLAB commands knowing the list of mesh node points p returned by distmesh2d command.
u = 1 - p(:,1).^2 - p(:,2).^2 trisurf(t,p(:,1),p(:,2),0*p(:,1),u,'edgecolor','k','facecolor','interp'); view(2),axis([-1 1 -1 1]),axis equal,colorbar
Next we can calculate the difference between the Finite Element approximation and the known solution to the poisson equation on the region bounded by the unit circle. Using MATLAB norm command we can calculate the L1 norm, L2 norm and infinity norm of the difference between approximated and known solution (U – u), where capital U is the Finite Element approximation and lowercase u is the known solution.
norm(U-u,1) gives L1 norm equal to 0.10568 norm(U-u,2) gives L2 norm equal to 0.015644 norm(U-u,'inf') gives infinity norm equal to 0.0073393
When we repeat this experiment using a finer mesh resolution we get the following results with mesh resolution values of 0.2, 0.15 and 0.1 which are passed as a parameter to the distmesh2d command when generating the mesh. As can be seen from the table below, a mesh with a finer resolution results in a Finite Element approximation that is closer to the true solution.
| Mesh Resolution | Node Count | L1 Norm | L2 Norm | L infinity Norm |
|---|---|---|---|---|
| 0.20 | 88 | 0.10568 | 0.015644 | 0.0073393 |
| 0.15 | 162 | 0.10614 | 0.012909 | 0.0032610 |
| 0.10 | 362 | 0.083466 | 0.0073064 | 0.0016123 |
Solving 2D Laplace on Unit Circle with nonzero boundary conditions in MATLAB
Next we will solve Laplaces equation with nonzero dirichlet boundary conditions in 2D using the Finite Element Method. We will solve \(U_{xx}+U_{yy}=0\) on region bounded by unit circle with \(\sin(3\theta)\) as the boundary value at radius 1. Just like in the previous example, the solution is known,
\(u(r,\theta) = r^3 \sin(3\theta)\)
We will compare this known solution with the approximate solution from Finite Elements. We will be using distmesh to generate the mesh and boundary points from the unit circle. We will modify the MATLAB code to set the load to zero for Laplace’s equation and set the boundary node values to \(\sin(3\theta)\). The following code changes are required:
The line
Fe=Area/3*4; % integral of phi over triangle is volume of pyramid: f(x,y)=4, load was 4 in poisson equation
from assembling F is changed to
Fe=Area/3*0; % integral of phi over triangle is volume of pyramid: f(x,y)=0, load is zero in Laplace
Also the line for setting the Dirichlet boundary conditions to zero
K(b,:)=0; K(:,b)=0; F(b)=0; % put zeros in boundary rows/columns of K and F
is changed to
K(b,:)=0; [theta,rho] = cart2pol(p(b,:)); F(b)=sin(theta.*3); % set rows in K and F for boundary nodes.
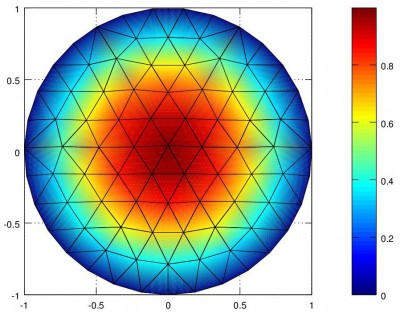
Running the non-zero boundary FEM code produced the result in Figure 5.
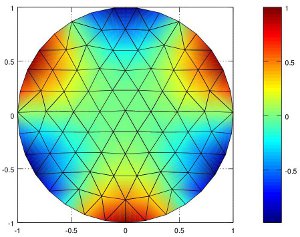
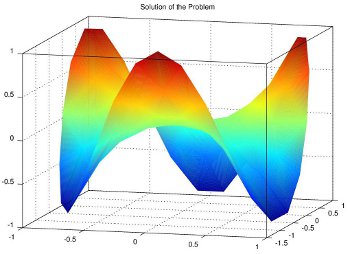
We can compare this result to the known solution \(u(r,\theta) = r^3\ sin(3\theta)\) of the Laplace equation with the given boundary conditions which is plotted below for comparison. We generated this plot with the following MATLAB commands given the list of mesh node points p.
[Theta,Rho] = cart2pol(p(:,1),p(:,2)); % convert from cartesian to polar coordinates u = Rho.^3.*sin(Theta.*3); trisurf(t,p(:,1),p(:,2),0*p(:,1),u,'edgecolor','k','facecolor','interp'); view(2),axis([-1 1 -1 1]),axis equal,colorbar
Comparing the Finite Element solution to Laplace equation with known solution produced the following results in MATLAB.
norm(U-u,1) gives L1 norm equal to 0.20679 norm(U-u,2) gives L2 norm equal to 0.035458 norm(U-u,'inf') gives infinity norm equal to 0.011410
Summary
- The Finite Element Method is a popular technique for computing an approximate solution to a partial differential equation.
- The MATLAB tool distmesh can be used for generating a mesh of arbitrary shape that in turn can be used as input into the Finite Element Method.
- The MATLAB implementation of the Finite Element Method in this article used piecewise linear elements that provided a good approximation to the true solution.
- More accurate approximations can be achieved by using a finer mesh resolution
- More accurate approximations can also be achieved by using a Finite Element algorithm with quadratic elements or cubic elements instead of piecewise linear elements.
nice article can u please send something on adjoint formulation of spn equations. It would be really helpful…………
Thanks
Documents très intéréssents. Je besoin la détail du code MATLAB de la méthode de volumes finis.
The code was based on code sample provided in section 3.6 of the book “Compuational Science and Engineering”. The matlab code is also available on this books website.
http://math.mit.edu/cse/
This online book about the finite volume method contains sample matlab code.
http://www.zums.ac.ir/files/research/site/ebooks/mechanics/introductory-finite-volume-methods-for-pdes.pdf
I have an interest to know mat lab software
Follow the FDM and FEM development. Is there any mistake? Solve the following problem. Write both the FEM and FDM solutions in MATLAB
K(∂^2 u)/(∂x^2 )-q=c ∂u/∂t
Heat transfer: k is thermal conductivity, C is specific heat
Groundwater flow: k is hydraulic conductivity C is specific storage
Diffusion: k is diffusion coefficient C = 1;
Hello, I like your article, it’s very good. I have a question for you : Have you already use the finite element method for imge processing ?
If you say yes can you show me how ?
Thanks !
Hi Ahdia, what specifically did you have in mind? Generally image processing is better handled by Finite Difference due to the regular data structure (rows and columns of pixels).
I am student of MS mathematics.i am work on Laplac equation by using the finite element method.I want to make MATLAB code for this method(Finite element method by using Laplac equation) so please help me because i face some problem for this code.
thanks for the code!
imho for dirichlet boundary conditions (unequal zero) the code should read:
% Implement Dirichlet boundary conditions U(b)=d at nodes in list b
K(b,:)=0; F(b)=d; % put zeros in boundary rows of K
Kb=K+sparse(b,b,ones(size(b)); Fb=F; % Stiffness matrix Kb (sparse format) and load vector Fb
I want to create Matlab program of 2 dimentional frame please tell me how to do it i am engineering student
I am not sure what you mean by “create Matlab program of 2 dimentional frame”. If you are asking how to create a mesh of different 2 dimentional shapes using matlab then see the distmesh tool for instructions.
http://persson.berkeley.edu/distmesh/
i am a phd student i have to generate mixed meshing for my problem in which the total plate is meshed by Q4 elements and at the center of plate there is a crack surrounding this crack i have to use triangular elements,how to generate this type of meshing using matlab code,pls tell me how to do this or give me some source to get this type of coding
For the triangular meshing part you can use distmesh tool in matlab. Have a look at the examples and documentation on this site.
http://persson.berkeley.edu/distmesh/
Also look at the function reference and published paper.
http://persson.berkeley.edu/distmesh/funcref.html
http://persson.berkeley.edu/distmesh/persson04mesh.pdf
For your problem you can probably use the dpoly function for the crack shape to list the points on the boundary of the crack and calculate the distance from the crack. As you can see in the examples the author puts shapes inside of other shapes to calculate distances for generating a mesh. You can for instance put a polygon shape like a crack inside a rectangle and then generate a triangular shape something similar for what he does in his examples.
% Example: (Square, with polygon in interior)
fd=@(p) ddiff(drectangle(p,-1,1,-1,1),dpoly(p,[0.3,0.7; 0.7,0.5]));
fh=@(p) min(min(0.01+0.3*abs(dcircle(p,0,0,0)), …
0.025+0.3*abs(dpoly(p,[0.3,0.7; 0.7,0.5]))),0.15);
[p,t]=distmesh2d(fd,fh,0.01,[0,0;1,1],[0,0;1,0;0,1;1,1]);
You can also use another dpoly instead of a drectangle for the outer boundary of the 2D distmesh shape.
For the Q4 elements you can use some other meshing tool to generate Q4 elements.
http://people.sc.fsu.edu/~jburkardt/m_src/quad_mesh/quad_mesh.html
Or you can write your own matlab code for this something like the first few lines of the MIT example in femcode.m
http://math.mit.edu/cse/codes/femcode.m
You will need to put a shape inside another shape for the region of the Q4 mesh. The inner boundary for the Q4 mesh will need to match the outer boundary of the triangular distmesh mesh so that you can connect these two meshes together. Distmesh has some routines for telling you the boundary points.
e = boundedges(p,t); % boundary edges
b = unique(e); % boundary points
I am not too familiar with meshing software packages but maybe your school has some other software for doing meshing.
is there any sample code of FEM by Cosserat model ( micropolar) ?
thanks
I need to mesh a code for meshing a curved plane with triangle,the equation of the plane is specified,in MATLAB
I’ve surfed the net but found noting
please help me
I need to solve poisson equation for a rectangle shape that has a sheet charge in the middle of that. how I can change this code for my structure?
i want to create a triangle using equation in matlab.
I need to write a matlab code to generate arbitrary triangular mesh for a rectangle. Does anyone know how to write the code in matlab?
Hi,
I have a question about 3D plot of our solution?
There is 3D plot of solution above, but I cannot find how to make it. Does someone know how to do it?
The 3D plot is made using MATLAB 3D plotting commands like mesh(x,y,z) or surf(…) for a 3D mesh or surface plot. See matlab documentation for details such as
http://www.mathworks.com/help/matlab/ref/mesh.html
and
http://www.mathworks.com/help/matlab/visualize/representing-a-matrix-as-a-surface.html
I am a PhD student in the heat transfer problem I am solving with MATLAB.
Conductivity of the matrix is equal to the page below. Constant heat source is applied to the page.
For the boundary conditions given below with the help of finite element software with 20 hexagonal nodal temperature values get resolved.
• The program is quite flexible so if Pzbr raise a few hundred or a few thousand German German small change can solve the problem (ie just get the number of elements along the x and y to resolve the issue).
• nodal values of temperature and temperature distribution contour is given as output.
• Naming variables and explained the program to understand it fully before.
I need to write a matlab code to generate arbitrary triangular mesh for a rectangle. Does anyone know how to write the code in matlab?
There is a link provided in this article to a matlab tool called distmesh for generating triangular mesh.
http://persson.berkeley.edu/distmesh/
Dear John,
I just can’t seem to figure out why this part
K(b,b)=speye(length(b),length(b)); % put I into boundary submatrix of K
appears in your code. Where do these ones come from?
When I derive the weak form of the given equations, and use Gauss’ Theorem to make it more simple.. I get one integral over the region and another one over the edge.
So does this identity matrix come from this edge integral? Although I assumed this would be zero…
This came from the finite element code in section 3.6 of the book “Computational Science and Engineering” by Prof Strang at MIT.
http://www-math.mit.edu/cse/
If you scroll down this page you will see a lot of MATLAB codes for material in the book and the MATLAB code for section 3.6 is the finite element code over a square region.
I also wrote another blog on Finite Elements using higher order elements which you might find helpful.
https://www.particleincell.com/blog/2012/finite-element-examples/
Here is his video lecture for 2D finite element over a circular region.
http://ocw.mit.edu/courses/mathematics/18-085-computational-science-and-engineering-i-fall-2008/video-lectures/lecture-27-finite-elements-in-2d-part-2/
He has a number of other lectures on Finite Elements in his course if you want to see how it is all derived.
That particular line appears in the original code and it look like for boundary nodes in U from KU = F, he previously zeroed out the whole row and column in K for boundary nodes and then he puts back in K the identity for boundary nodes. This is because U contains boundary nodes and 1*U(b) = F(b) is just saying set the boundary nodes to their boundary values F(b).
i need to solve pde b vp by finite element method please help me
What equation are you solving?
i need matlab code for finding stress temp displacement 2d 3d heat transfer
How can we change the rectangular shape to an L-shape in matlab and then solve the steady state heat problem by Laplace equation using FEM with boundary conditions?
Hi Hazem
You can create an L-shape using “distmesh” mentioned in the article. Go to the distmesh website and look at the polygon example for how to create mesh for an L-shape.
http://persson.berkeley.edu/distmesh/
It gives the following example for a polygon.
pv=[-0.4 -0.5;0.4 -0.2;0.4 -0.7;1.5 -0.4;0.9 0.1;
1.6 0.8;0.5 0.5;0.2 1;0.1 0.4;-0.7 0.7;-0.4 -0.5];
[p,t]=distmesh2d(@dpoly,@huniform,0.1,[-1,-1; 2,1],pv,pv);
Then get the list of boundary points using
b=unique(boundedges(p,t));
You can set the boundary points to whatever value you want your boundary points to have. For example I set the boundary values to the values of a sine wave in one of the examples in the article.
F(b)=sin(theta.*3);
hi,john,I want creat a crack in a rectangle plate.how can do it by distmesh,please.
Hi James
You can find out how to do it by looking at the examples and documentation on the distmesh site. Look at example 4 on page 10 and 11 of this document.
http://persson.berkeley.edu/distmesh/persson04mesh.pdf
The sample code he gives is
);
(4) Polygons. It is easy to create dpoly (not shown here) for the distance to a
given polygon, using MATLAB’s inpolygon to determine the sign. We mesh a regular
hexagon and fix its six corners:
>> phi=(0:6)’/6*2*pi;
>> pfix=[cos(phi),sin(phi)];
>> [p,t]=distmesh2d(@dpoly,@huniform,0.1,[-1,-1;1,1],pfix,pfix);
Note that pfix is passed twice, first to specify the fixed points, and next as a parameter to dpoly to specify the polygon. In plot (4), we also removed a smaller rotated
hexagon by using ddiff.
He uses ddiff to cut out a shape inside another shape. So you can probably use ddiff with a rectangle and a polygon shape for the crack.
I want to do finite element analysis of composite plates.But since i am a fresher to matlab i am unable to do. Please can somebody provide me simple problems solved in matlab.
john
I find the post extremely helpful to mesh the geometry that I am working in. But connecting this with psi-omega equations of the Navier Stoke’s equations with 2D incompressible fluid flow is difficult for me. Any help?
how to analyze numerical weather prediction using FEM?
Hi,
Thanks for this, it has been very useful.
Just a note, this routine is a LOT faster if you create the sparse K matrix AFTER the element loop, as described here under Method 3: http://imechanica.org/node/7552.
Catherine
Hi,how do you determine which nodes are boundary nodes?
Looking at the distmesh function reference
http://persson.berkeley.edu/distmesh/funcref.html
you can get the boundary point list as the unique points returned by boundedges function for the boundary edges.
e = boundedges(p,t);
b = unique(e);
b contains the list of boundary points.
How to calculate the u(x,y)? where (x,y) is not the node.
Look at the P1 Linear Elements mentioned in this post.
https://www.particleincell.com/2012/finite-element-examples/
and the continuous Galerkin method mentioned in the post.
U(x,y) = U1 * phi_1 + U2 * phi_2 + U3 * phi_3
where U1, U2, and U3 are the values at the node and U(x,y) is inside the triangle. The basis functions for the triangle, (phi_1, phi_2, phi_3) are calculated as explained in the P1 Linear Elements section.
When setting the Dirichlet boundary conditions to cart2pol(p(b,:)), I recieve a MATLAB error that the coordinate y is not specified. Do you happen to know why this happening?
Error in ==> cart2pol at 22
th = atan2(y,x);
No I don’t know why it is happening. But instead of
[theta,rho] = cart2pol(p(b,:));
you might try using
[theta,rho] = cart2pol(p(b,1),p(b,2));
where you explicitly provide the y coordinate as p(b,2) . Also try looking at the cart2pol documentation in matlab.
http://www.mathworks.com/help/matlab/ref/cart2pol.html
Hi, May I know if it is possible to adapt the code to neumann boundary condition equals to 0? Sorry I am new to FEM
I am M.Sc. student know I went to apply project work on a Matlab code for ” a comparison of weak and discontinuous galerkin finite element methods for solving second-order elliptic boundary value problems”? sorry I am new to Galerkin finite element methods using matlab code
I need to write a matlab code to solve
2D heat conduction in irregular geometry with structured mesh. Does anyone know how to write the code in matlab?
Mohammed, not quite what you are looking for, but this post talks about solving advection-diffusion equation on the Cartesian mesh. I may add the FE version the future. Diffusion equation is the heat equation. Also, what do you mean by irregular geometry with structured mesh. Do you mean cut cells and Cartesian mesh, or a body fitted mesh like in this mesh generator example?
I am working on a paper, entitled “A block alternating splitting iteration method for a class of block two-by-two complex linear systems”. In this paper, an optimization problem is discretized by finite element. I have emailed authors of paper and asked them to
send me matrices of the problem, but did not receive a response. I would be grateful if one can help me.
Hello, Can anyone help with simple matlab code for discontinuous Galerkin method for poisson problem in 2D. Using Gaussian quadrature for computing and assembling the interior contribution is somehow difficult for me. I am using Beatrice Reviere book as a reference.
Thanks alot
hello
can any one give me matlab codes for my dissertation work.
my topic is numerical modeleing of groundwater artificial recharge in unconfined aquifer,
so related to this any code i needed.
pleassssssss
its very ipm for me
can you send me a full discribtion of wave equation in 2D with euler implicit method that solved in MATLAB.
thanks.
KIND REGARDS.
Atefe, if you send me a mail I’ll send you the Matlab code.
thanks alot Peter.
my email is
a.dehghannayyeri@gmail.com
hi peter, i have a request for. as i determined you sent atefe 2-d wave equation codes,would you please send me too and if you have send me matlab codes for finite element solution of i-d wave equations.
Best regards
Hello
I am a degree student and I am developing a code in order to solve the fluid flow in a pipe and later on in a curved channel. Characteristics of the fluid are: using FVM, cell-centered for pressure and face-base for velocity, incompressibility, stationary. The main problem that I have is how to solve the momentum equation because I don’t know how to create the matrix. I was checking many programs that use Kron function but I don’t understand the how it works.
Thanks in advance
Hi Daniel
kron is the Kronecker product. Have a look at the 17 minute mark of this video for a description of it being used in an MIT lecture.
http://ocw.mit.edu/courses/mathematics/18-085-computational-science-and-engineering-i-fall-2008/video-lectures/lecture-26-fast-poisson-solver-part-2-finite-elements-in-2d/
John
Thank you so much. I saw the video and it was very useful and interesting. I was following this professor because is deeply related with the topic of my thesis.
I have the problem that I don’t know how to solve the momentum equation. I am trying to solve this problem using the SIMPLE algorithm. Characteristics of the fluid are laminar, viscous.
The boundary conditions that I have is like a pipe, North and South face are both walls and West will be the inlet and east the outlet. I know the velocity field that I would establish as linear and parabolic.
At the beginning, I guess an initial pressure with values:
1 in the inlet west face
0 in the oulet east face(atmosferic pressure)
1 in the north face
1 in the south face
and after I have to solve the momentum equation for u and v the dilemma is because I don’t know which is the best way to solve this equations with the most efficient way.
Thank you in advance,
Daniel
I am not that familiar with CFD problems and FVM but here is a link to a good resource for it with some FVM matlab code in the appendix.
http://www.zums.ac.ir/files/research/site/ebooks/mechanics/introductory-finite-volume-methods-for-pdes.pdf
Maybe this link can help you.
John
I am a Msc. student and it is an interesting and usable implementations for two dimensional steady problems. But I will not have to understand the codes for two dimensional and time dependent problems like
U_t-U_{xx}-U_{yy}=f(t,x,y), please tell me a matlab code if you have an idea for these type of problems with some initial conditions and boundaries.
My reply the the question just before yours had this link
http://www.zums.ac.ir/files/research/site/ebooks/mechanics/introductory-finite-volume-methods-for-pdes.pdf
and it talks about time dependent problems and has some matlab code in the appendix.
Hello Dear,
Thank you for your last reply and I am ask one other question concerning the matlab code to solve advection diffusion equation using finite element method, please would you have to help on it.
Thanks a lot
hello.I am a PhD student. I want MATLAB code for discontinuous Galerkin method for Poisson’s equation.Please send to me. Thanks
Sorry, I don’t have such a code available.
This book might have some MATLAB code for discontinuous galerkin method.
http://epubs.siam.org/doi/book/10.1137/1.9780898717440
In the description it says.
“Appendices contain proofs and MATLAB® code for one-dimensional problems for elliptic equations and routines written in C that correspond to algorithms for the implementation of DG methods in two or three dimensions.”
i’m working on meshfree method.and i cant understand it plz tel me any idea.
I found this page incredibly helpful when trying to program the FEM for a Poisson Equation using rectangular elements instead of triangular ones, but only for constant f(x,y), like in the examples above. Do you know how I could modify the code in order to analyse a value of f(x,y) such as 6xy(1-y)-2x^3?
Look at the last example with the heading
“Solving 2D Laplace on Unit Circle with nonzero boundary conditions in MATLAB”
the f(x,y) was set to sin(3*theta)
The blog indicated that the following was changed for this example and code is provided in the link.
“””
Also the line for setting the Dirichlet boundary conditions to zero
K(b,:)=0; K(:,b)=0; F(b)=0; % put zeros in boundary rows/columns of K and F
is changed to
K(b,:)=0; [theta,rho] = cart2pol(p(b,:)); F(b)=sin(theta.*3); % set rows in K and F for boundary nodes.
“””
Also there is another blog
https://www.particleincell.com/2012/finite-element-examples/
with a number of examples and some have set f(x,y) to some function of x and y and the code is provided in the link.
John
Hi.
Thank you for this page.
Do You have any example with creep behavior ?
Thanks !
Hi.
I need Matlab code for 2D Triangular element with 6 nodes (Linear Strain Triangle (LST)) with concentrated or distributed load.
Could you please help me in this way?
Hi.
I need Matlab code for 2D or 3D a weak Galerkin finite element method for nonlinear convection-diffusion problem
Could you please help me in this way?
Hi.
I need Matlab code for 2D or 3D a weak Galerkin finite element method for nonlinear convection-diffusion problem
Could you please help me in this way?
Hello, I need matlab code for 2D moment frame structure(2 story 2 span) for gaining mode shape and farequency.
or any various example for 2D moment frame
Could you please help me?
Thank you
Hello, I need matlab code for 2D moment frame structure(2 story 2 span) for gaining mode shape and frequency.
or any various example for 2D moment frame
Could you please help me?
Thank you
WHAT IS THE ANALYTICAL SOLUTION OF LAPLACE EQUATION IN A UNIT CIRCLE?
HELP ME TO SOLVE THE LAPLACE EQUATION IN 2D USING FINITE ELEMENT USING HEXAGONAL ELEMENT?
i have an error in this line:
grad=C(2:3,:);Ke=Area*grad*grad; % element matrix from slopes b,c in grad
any suggestion guys?
That line if found in the original code from section 3.6 of the book “Computational Science and Engineering”
http://math.mit.edu/~gs/cse/
The line of code you mentioned is found in this code from section 3.6 of the book.
http://math.mit.edu/~gs/cse/codes/femcode.m
Try running this matlab program and see if you are still having a problem with that line of code.
i need help pleace ,
I want to change the line for setting the Dirichlet boundary conditions form zero to T(0,y)=0℃,T(1,y)=200y℃
T(x,0)=0℃ ,T(x,1)=200x℃
in (femcode.m)
Can anyone help me
The boundary points b in the code are given in the line
b=[1:m,m+1:m:m*n,2*m:m:m*n,m*n-m+2:m*n-1]; % bottom, left, right, top
% b = numbers of all 2m+2n **boundary nodes** preparing for U(b)=0
If you want to set right and top to 200 then you can specify the right boundary as br and the top boundary as bt
br=[2*m:m:m*n]; % right boundary node numbers
bt=[m*n-m+2:m*n-1]; % top boundary node numbers
Then in the code where the boundary values are set
K(b,:)=0; K(:,b)=0; F(b)=0; % put zeros in boundary rows/columns of K and F
K(b,b)=speye(length(b),length(b)); % put I into boundary submatrix of K
you can insert the lines
K(br,:)=0; K(:,br)=0; F(br)=200; % put 200 on right boundary
K(bt,:)=0; K(:,bt)=0; F(bt)=200; % put 200 on top boundary
before the line
Kb=K; Fb=F; % Stiffness matrix Kb (sparse format) and load vector Fb
With these changes you will have a value of 200 on the right and top boundaries.
I am Msc student in Hawassa university in Ethiopia. Now i need to do my thesis on contaminant transport through porous medium by finite element method. would you help me by some matlab codes please?
I need to do my thesis on Numerical simulation of contaminat transport through groundwater flow through finite element method. how can you help me
Sorry I can’t help you with that.
Hi.
I need Matlab code for 2D or 3D a finite element method for advection diffusion equation
Could you please help me in this way?
No I don’t have finite element code for advection diffusion equation. I know of a Finite Volume code for 2D advection from appendix C of this online book.
http://zums.ac.ir/files/research/site/ebooks/mechanics/introductory-finite-volume-methods-for-pdes.pdf
Here is the matlab code for it.
http://www.mathworks.com/matlabcentral/mlc-downloads/downloads/submissions/35363/versions/2/previews/FVlinearadvectionFOU2D.m/index.html
Reply
No I don’t have finite element code for advection diffusion equation. I know of a Finite Volume code for 2D advection from appendix C of this online book.
http://zums.ac.ir/files/research/site/ebooks/mechanics/introductory-finite-volume-methods-for-pdes.pdf
Here is the matlab code for it.
http://www.mathworks.com/matlabcentral/mlc-downloads/downloads/submissions/35363/versions/2/previews/FVlinearadvectionFOU2D.m/index.html
Hi Dear.
Thank you for your help.
I need Weak formulation and Matlab code for 2D a finite element method for coupled partial differntial equation or system of partial diferential equation of two variables x and y.
Could you please help me in this way?
No I can’t help you. The only Finite Element code I have is what I wrote about in the blog posts on this site. You will need to look somewhere else to find what you are looking for or develop your own matlab code to do what you want it to do.
Please help me giving 1D advection, advection dispersion matlab codes to simulate solute transport in groundwater by FEM
I do not have such a code. You will need to look somewhere else.
Ok. What about fem solution of time dependent 2d diffusion eqn? and simple 2d advection eqn? by fem? please
Sorry, I don’t have any FEM examples. Why do you need FEM? Can you just use Finite Volume? That’s much easier to implement.
can you please send me some example of matlab code related to finite element method in electrical engineering or some data related to my field
can someone help me to solve photon diffusion equation using FEM for a circular mesh where a circular inclusion inside the circular mesh
How would you change this code for using the 2d heat equation instead of poisson?
Emily, steady-state heat equation is the same as Poisson’s equation. The only difference is the forcing vector being generally zero (i.e. Laplace equation).
Hello, In your code, only the stiffness matrix and force vector are constructed.
My question is how to formulate the mass matrix in the case I consider the effect of inertia force.
Thanks!
Hello, after using distmesh for mesh generation, the selection of boundary nodes is possible for simple shapes, but if it is a combination of graphics, such as square coaxial line, there is also a circle in the rectangle, this kind of graphics can be divided into internal and external boundary nodes, how to distinguish internal and external boundary nodes when screening, because When adding boundary conditions, it is necessary to distinguish internal and external conditions.
If this is a question about distmesh maybe you can ask your question to the creator of the distmesh software. See distmesh website for the creator’s email address
http://persson.berkeley.edu/distmesh/