Effect of Ion Thruster Plume-Thermosphere Interaction on Satellite Aerodynamics in Very Low Earth Orbit

This article was submitted by S. Andrews now at Advanced Space Propulsion Group, Department of Industrial Engineering, Università degli Studi di Padova, and his advisor L. Berthoud at Department of Aerospace Engineering, University of Bristol to to highlight a thesis work that utilized our Starfish plasma simulation code. Let us know if you have other Starfish-related research that you would like to highlight.
Satellite operations in Very Low Earth Orbit (VLEO), altitudes below 250km, are highly appealing for flexible, high-performing and economical spacecraft operations to deliver low-cost communications and Earth observation data. However, the mission lifetime in VLEO is significantly limited due to the aerodynamic drag from the momentum exchange between the residual atmosphere and satellite. The high specific impulse of ion thrusters allows continuous compensation for the variable deceleration experienced by a satellite due to the atmospheric drag, without the vibrations and limited total mission impulse with the use of conventional chemical engines. The on-board propellant required is proportional to the mission , the budget for which is given by the total mission drag. The objective of this work was to assess whether base-flow interactions with the ion thruster plume, in particular the charge-exchange (CEX) cloud, modify the properties of the thermospheric flow about VLEO satellites to have significant impact on the value of the satellite drag coefficient . The system of interest in given in Figure 1.
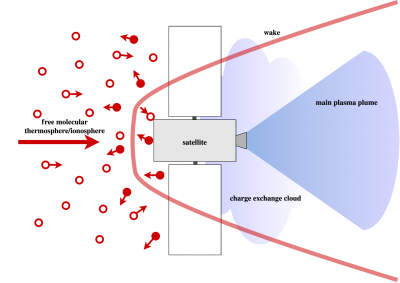
The plume expands into the rarefied free-molecular thermosphere, therefore requiring a coupled DSMC-PIC implementation in Starfish. The system was considered as four species subsets: propellent neutrals/ions, which in this work was ??/??+ and ambient thermospheric neutrals/ions. The thermospheric model used in this study is comprised of the primary species found in VLEO; ?, N2, O2, ?, ??, ?? and ?. In principle, it was possible to employ fully-kinetic PIC simulations, but to do so on the length scale required to allow the thermospheric wake to converge downstream of the satellite would have been computationally infeasible. The quasi-neutral approach offers extremely rapid computation of plasma potential in the plume but would not correctly resolve potential drop in the non-neutral satellite sheath or low density CEX region. Since the CEX cloud was assumed to dominate the interactions on the base-flow, a combined “Poisson switch” method was developed. Prior to commencing the solver iterations, the local Debye length at each node of the domain is calculated. If λ? < Δ?,Δ?, the node was flagged as quasi-neutral and potential on it obtained by the direct Boltzmann inversion. The non-linear Poisson solver then backfilled the remaining region.
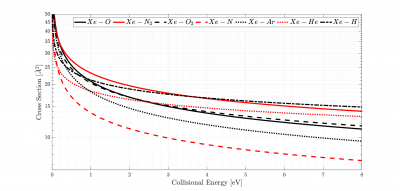
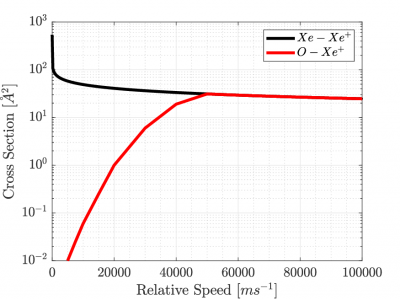
To correctly capture the interactions, an accurate collision model was critical. The variable hard sphere (VHS) model was used for neutral collision cross-sections as per standard dynamics of DSMC. Figure 2 shows that most probable collisions with Xe are ?2 and ?. ?2 is one of the most concentrated species in VLEO (the other being ? ). The density of ? is ?(105) lower. Xe CEX collisions were modelled with the MCC approach using the well-established relationship from Rapp and Francis. The cross-section for CEX collisions between ??+ and thermospheric species had not been measured in previous works. CEX occurs when the defect energy in a collision Δ? is near-zero. A plug-in to Starfish calculated Δ? and if Δ? < 0, collisions were assumed MEX and handled by the DSMC routine. Else, for Δ? ≥ 0, the CEX was modelled, with the maximum CEX cross section estimated with the theoretical relation of Sack et. al. This approach for ??+ −? showed good agreement with the resonant cases of ?+ − ?, as shown in Figure 3.
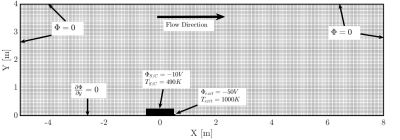
The satellite was taken to be a cylinder of 1m length and a frontal area of 0.25m2, with surface temperature of 490K and surfaces isotopically conducting with floating potential fixed to −10? to approximate spacecraft charging in VLEO. Gas-surface interactions were assumed to be fully diffuse with complete thermal accommodation to the satellite walls. The simulations were performed on the XY half-domain in Figure 4, given both the thermosphere and plume are axis-symmetric. Thermosphere flow enters the left-hand boundary as a Maxwellian source. The ion thruster ion and neutral population were taken to be Maxwellian sources using the operating conditions of the Qinetiq T5 GIE. Simulations were performed for 10km increments between 160km and 250km. The drag was calculated by directly summing the momentum lost by particles impacting the satellite surface at each time-step. An initial value of thrust was set as equal to the clean satellite drag, calculated from simulations in absence of the thruster. Since the presence of the plume was theorised to change the gross drag, at every 1000?ℎ time-step the thruster exhaust parameters were updated such to reset the thrust equal to the drag measured at that time-step in the simulation. All simulations converged to an equilibrium drag-compensating thrust before 35000 time-steps of 1.2×10-6s. The wall-clock time required to run each case was 7-29hr on 16 2.6GHz cores of the BlueCrystal Phase 3 supercomputing cluster, run by the High Performance Computing Centre at the University of Bristol.
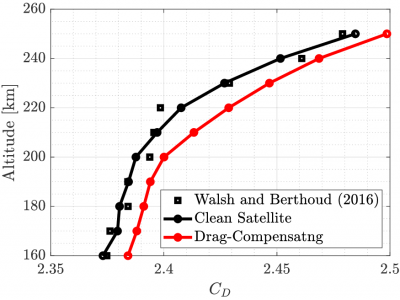
Firstly, the ??+ and ?? back-flow is greatly reduced over vacuum cases and scales linearly with the ambient thermospheric density. Figure X shows the difference in the plume ion density at 250km compared to a vacuum case. Secondly, the satellite wake refill is delayed due to collisions between CEX ions and thermospheric species, proportional to the relative difference between the ambient number density and the concentration of the near-exit CEX cloud. The CEX cloud is partially picked-up by the thermosphere and propagates downstream. ?? inclusive of thruster interactions was seen to be greater at all altitudes in the VLEO range as shown in Figure 5. This is driven by an overall increase in pressure drag as the near-exit plume structure is of sufficient density to deflect the freestream but not to account for wake refill, and shear stress variation according to the collisions between plume backflow and thermospheric species, at parallel satellite surfaces, reducing the incoming velocity and increasing local density. Although the increase appears small, such an increase in drag accumulates over the mission such that the satellite re-entry may be many days prior to original estimates.
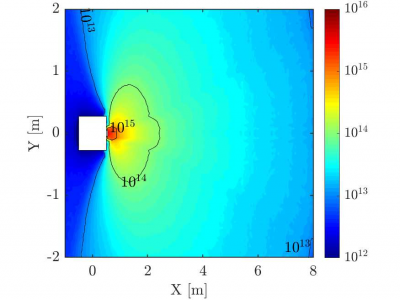
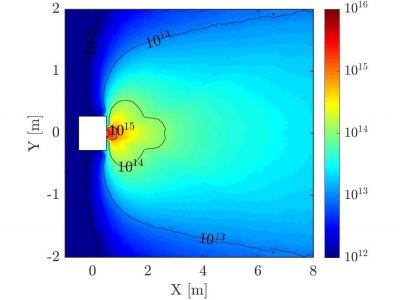
This study has shown that effects of ion thruster interactions in VLEO should be included in future analyses, to ensure drag models are complete and accurate fuel budgets are made. It is also prudent to state that with the reduction in plume back-flow observed in the thermosphere, the usual detrimental effects associated with CEX ion-spacecraft interactions (recombination, charging, erosion) are of lesser concern. The use of a satellite surface potential of -10V may have been a conservative assumption, and the true charge in VLEO may be considerably less, decreasing the strength of the plume-to-satellite plasma sheath and reducing back-flow further. Finally, future work shall focus on addressing the effects of some phenomena and mission features that have not been included in this study, such as: (I) different satellite geometries, (II) Earth magnetic field (affecting the plasma plume expansion), (III) self-consistent surface charging and (IV) different thruster models (including air-breathing and Hall effect thrusters).
For more information please see:
- S. M. Andrews & L. Berthoud, “Characterising Satellite Aerodynamics in Very Low Earth Orbit inclusive of Ion Thruster Plume-Thermosphere/Ionosphere Interactions”, Acta Astronautica, vol. 170, pp. 386-396, Jan. 2020, doi:10.1016/j.actaastro.2019.12.034 (link)
- S. M. Andrews & L. Berthoud, “Effect of Ion Thruster Plume-Thermopshere Interactions on Satellite Drag in Very Low Earth Orbit”, Proceedings of the 70th International Astronautical Congress, Washington D.C., USA, Oct 2019, IAC-19,C4,5,1,x54388 (link)
- S. M. Andrews & L. Berthoud, “Modelling and Characterisation of Plasmadynamic Drag on Gridded Ion Propelled Spacecraft in Very Low Earth Orbit”, Proceedings of the 69th International Astronautical Congress, Bremen, Germany, Oct 2018, IAC-18-E2.2.10.x48637 (link)