Simple Particle In Cell Code in Matlab

Introduction
This post includes the sample Particle-In-Cell (PIC) code that goes with our previous article on the electrostatic particle-in-cell method. It simulates the flow of uniform plasma past an obstruction – a charged plate in our case. This simple code is implemented in Matlab. If you don’t have Matlab, you can run the code using Octave, which is an open-source Matlab emulator. If you do end up getting Octave, as of the date of this article, the MinGW build available on Octave-Forge is out of date and contains a buggy contouring function. In order to use the latest version – and see the plots – you need to install Cygwin and add Octave as a Cygwin package…
File Organization
The sample PIC code is contained in two files: flow_around_plate.m and eval_2dpot_GS.m. The first file is the actual PIC code, while the second file holds the potential solver. The solver computes electric potential using the Finite Difference method. The code simulates the flow of solar wind (low density plasma) over a charged plate. The code is not particularly fast (it’s in Matlab after all!), but shouldn’t take more than few minutes to run on a standard PC. If you run the code through Octave, make sure to first execute more off to avoid pagination of the output.
Input Parameters
The simulation plasma environment is set on lines 24-28:
n0 = 1e12; %density in #/m^3 phi0 = 0; %reference potential Te = 1; %electron temperature in eV v_drift = 7000; %ion injection velocity, 7km/s phi_p = -7; %plate potential
By changing the plate potential, you can alter the size of the wake that forms behind the plate. At sufficiently large values, ions are attracted back to the plate. This behavior is analogous to the plasma environment that forms around satellites utilizing electric propulsion. Slow moving ions are extracted out of the thruster plumes and can impact surfaces without a direct line of sight to the thruster.
The simulation domain size and the number of time steps is set starting with line 35:
nx = 16; %number of nodes in x direction ny = 10; %number of nodes in y direction ts = 200; %number of time steps
At the default settings, 200 steps is sufficient to reach steady state. The simulation time step is such that a particle traveling at the drift velocity will cross 10% of the cell length per time step. Since particles speed up as they approach the plate, this conservative time step keeps particles from traveling more than a cell per time step. This is a necessary constraint in all PIC codes, but in general you want to keep the particles traveling a shorter distance (I generally use 25% in my simulations). The number of particles generated at each time step is specified on line 39,
np_insert = (ny-1)*15; %insert 15 particles per cell
Plate dimension are set on lines 48 and 49:
box(1,:) = [floor(nx/3) floor(nx/3)+2]; %x range box(2,:) = [1 floor(ny/2)]; %y range
For an explanation of the physics used in the code, please see the Particle In Cell page. Feel free to leave a comment if you have any questions.
Download
Download the files here: flow_around_plate.m, eval_2dpot_GS.m
You may also be interested in a Finite Element Particle In Cell example.
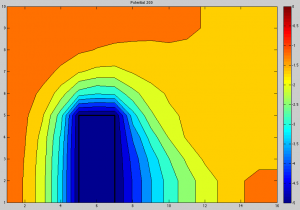
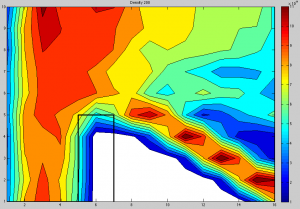
Please leave a comment if you have any questions. Thanks!
Hi Lubos;
in Matlab code your code the wall potential is given phi_p = -7V. Is there any special meaning under this or was it chosen randomly,
and, what is the result of choosing positive wall voltage?
Thank you..
Best regards,
Hi Ozgur,
Yes, this is just some arbitrary value that produced nice looking plot. The potential is negative since the potential in the bulk plasma is zero and hence this attracts the ions towards the plate. If you chose a positive value, the ions will be repelled away.
Our professor assigned us an assignment on Particle in Cell simulation for his Plasma Engineering graduate class. We are supposed to use your code as a basis. After altering your code a bit, we basically moved and extended the wall/barrier to the right edge and changed a few parameters.
Is there something in your code that generates a decrease in the density on the left hand side of your density plot? Since there’s a uniform injection of ions, shouldn’t there be a uniform density until it reaches the sheath region? We just can’t really understand why the left hand side is also going to zero since it’s technically not supposed to do that. In your density plot online, it seems that the density goes to zero, as well, so maybe we’re not wrong, I just don’t understand why.
Hi Ashley, that has to do with the way particles are injected into the domain. The particles are born at a random “x” position in the first cell and also with a random velocity. So you basically end up with a non-uniform density in this first cell. You can avoid this by loading particles at x=0 and also doing the density update prior to the push. I left it this way since I didn’t think it made much difference on the solution at the plate location.
Hi Lubos,
i try to simulate plasma flows by using Particle in Cell method. The situation is very similar to your matlab code.;(i.e. collisionless and quasi neutral plasma,and the model is hybrid). i have finished the code in non-rectangular domain. But i could not verified the results whether true or not. Can you help me about verification.
Thank you very much for your attention.
Sure Ozgur, what did you have in mind? Some ways you can also try to verify your code is by testing the potential solver with some analytical function and also checking for energy conservation.
A PIC code in Matlab could be adapted to run in a computer cluster? and/or adapted to run in parallel?, Thanks
Hi Sergio, if I am not mistaken, Matlab now supports parallel processing. However, I am not familiar with it – we do most of our actual development either in C/C++ or Java. Matlab is a great prototyping language, but if you are after speed, you’ll be better off using a non-interpreted language.
Hi…I am new in PIC..I want some help how to do assignment from particle position to grid position…how I can implement…
Also how I may know how many particle are there in one particular cell of the whole geometry?
I want to interpolate particle properties like velocities and charge to my grid (one dimensional only)
As in each cell there are so many particles so each has it own contribution on particular node (let say k) depending on weight factor so I want to know how I can sum all those properties on a node (k and k+1).
Why you have add 1.0 in the assignment part (fi = 1+part_x(p,1)/dh; )?
Please elaborate the assignment part.
Please help me…
Regards
Amitavo, you basically want to compute the average velocity. This is no different from computing the regular average, with the difference that you are averaging fractional contributions. When you scatter data to the grid, you place a fraction of the velocity on the left node, and the rest on the right node, assuming 1D problem. So as an example, let’s say the velocity is 100 m/s. Perhaps the particle is really close to the right node, so the right node may get 90 m/s, while only 10 m/s is deposited to the left node. Next imagine that this cell contains 5 particles, and that they are all located at the same spatial position. You will end up with 450 m/s total velocity on the right node and 50 m/s on the left node. If you were to divide the velocity sum by 5, you will get that the velocity varies from 10 m/s on the left end to 90 m/s on the right end. This is clearly incorrect since all particles in the cell are at 100 m/s. To get the correct answer you need to divide the sum by the fractional particle count. This is why you want to also keep a “count” variable on the grid nodes to which you scatter the value of 1 (if all particles have equal weight) for each particle. If particles have a variable weight than you scatter the respective specific weight. You then divide each node value by the count, i.e. vel[i]=vel_sum[i]/count[i];. In this example, the counts would be 4.5 on right, and 0.5 on left, giving you 100 m/s on both the left and the right node.
The second question about adding 1 is due to Matlab starting its indexing at 1 instead of 0. If your code is in C or Java, you don’t add this 1.
tHANKS FOR YOUR NICE REPLY. YES NOW IT IS UNDERSTAND THAT I AM WRONG IN AVERAGING.
BY “COUNT”..I UNDERSTAND THAT I HAVE TO MAKE COUNT OF NO. OF PARTICLES CONTRIBUTION OF PARTICULAR GRID…
BUT STILL “COUNT” STATEMENT IS NOT VERY CLEAR TO ME SO THAT I CAN IMPLEMENT IT….COULD YOU PLEASE MAKE CLEAR TO ME WITH AN SMALL EXAMPLE….IT HELPS ME TO CLEAR MY UNDERSTANDING…
It’s no different than scattering velocity, except that you are scattering particle weight. If all particles have the same weight, you simply scatter the value of 1.0 every time you scatter the velocity. If they have different weights, you scatter the particle weight, or the weight divided by a reference weight (to normalize, since weights are typically very large numbers).
Thanks a lot….
I am facing problems in assingment process after pushing the particles.
I am not able to implement the particle properties from the new position of the particles to the grid point which is shared by two cells.
After the localization process for the new particle positions how I can implement the assignment operation?
Please guide me as I am new in the field.
As an example: Suppose we have 10 particles in (K,K+1) cell and 5 particles in (K-1,K) cell after pushing then I want to assign velocities and charge to K node due to all these particles. Please suggest me/ help me how can I perform this operation.
Regards
Hi,
I have found your writings very useful. I am learning plasma out of interest. I have a doubt: if I have a 2d plasma inside 4 walls of 0 Volt each and I want to plot the potential (calculated as in your tutorial, electrons as Boltzmann particle, ions : moving macroparticles), why do I get an inverted Gaussian type curve? I thought potential should be uniform across a plasma! Thanks.
Hi John, that would be the case if the governing Poisson equation reduced to the zero forcing function Laplace form, $latex \nabla^2\phi=0$. However, that is not the case. Even though plasma is quasi-neutral, this condition does not hold in the vicinity of walls. Near the walls you will get what’s known as a sheath, where $latex n_e
Am working on simulation of DBD using particle in cell method.PLS Sir how will i go about it.
That’s not a particularly easy problem. I must admit I do not have much background with modeling discharges (most of my work has been in plume modeling), however what I imagine you would need is a code that takes into account dielectric charging, surface deposition, as well as a model for breakdown. Have you seen the excellent book by Lieberman and Lichtenberg, Principles of Plasma Discharges and Materials Processing? It goes into details of various plasma discharges.
Hi,
Thanks for the explanation. If the electrons are also simulated as macroparticles like ions (with same specific weight but with opposite charge), what is to be done for the sheath formation in the simulation? Or, will it be inherent? How the time-step will be defined then?
Secondly, in the Matlab code for flow around a plate, why the factor 0.5 is missing for x-component of velocity in the Particle Generation section of the code? It is there for y-component of velocity.
The sheath will form self-consistently. It forms since the electrons are more mobile (lower mass -> higher velocity) and thus will be absorbed by the wall faster than the ions. This will in turn make the wall negative in respect to the bulk plasma (or the plasma potential will go up if the wall potential is held fixed). This potential gradient acts to reduce the electron flux. The wall potential will continue to go down until the electron current is balanced by the ion current. About your second question – good catch! I have no idea. It could very well be a typo. The way it’s written you will end up with anisotropic temperature. I wrote the code few years ago so I don’t quite remember what I was thinking back then.
Thanks for your reply. Also, thank you for maintaining such an active website.
If you had an unstructured triangular mesh instead of a mesh with quadrilateral elements, what would be a good algorithm for calculating the electric field at each of the mesh nodes. For the scatter and gather operations I was thinking you could use barycentric coordinates of a triangle.
http://en.wikipedia.org/wiki/Barycentric_coordinate_system_(mathematics)
But once you have the potential at each of the nodes on an unstructured mesh, what would be a good way to calculate the E field at each node.
This is really the foundation of the finite element method. Typically what you do is you define a basis element for each cell. These elements can be of different order. The derivative will be one order less. Quite typically, you may see linear elements used for potential which then give you zero-order (constant) electric field in the cell.
I tried implementing this PIC code using the finite element method solver from this blog post.
https://www.particleincell.com/2012/matlab-fem/
Here are some results I got.
https://dl.dropbox.com/u/5095342/Images/figure1.jpg
https://dl.dropbox.com/u/5095342/Images/figure2.jpg
https://dl.dropbox.com/u/5095342/Images/figure3.jpg
However, in order to get a stable result I needed to set
Te = 0.125; %electron temperature in eV
instead of Te = 1.0; . When I do this I get a result that looks similar to what the original PIC code from this blog post generates with Te set to 0.125 .
Do you know why the solver result might become unstable when Te is set higher than 0.125 ?
I used the following in the MIT FEM code for f(x,y).
% multiply Fe by f at centroid for load f(x,y): one-point quadrature!
Fe=Area/3*((mean(den(nodes,1))-n0*exp((mean(phi(nodes,1))-phi0)/Te))*QE/EPS0);
Does this look correct to you?
Hi Dr. Brieda
I have some question about ES-PIC code. Please help me.
In your code, was electron and ion isothermal together? otherwise What is your scientific reason?
How have been calculated time step (10^-12) for electrons?
Why the drift velocity has been considered only for ions? note that 10^5 (order of thermal velocity of electrons) isn’t much larger than 10^3 (order of drift velocity)
in calculation thermal velocity , vth=k*Te/m was used, in spite of temperature of electron was in ev not Kelvin!
best regards
Hi Mahzan, these assumptions are typically taken in the context of plume modeling. The reason is that including electrons as kinetic particles (or even a fluid) complicates the numerical model unnecessarily. If magnetic field is not present, the electron density follows the Boltzmann relationship.
Thanks for catching that vth mistake, I have corrected it. I have also specified a different temperature for ions to indicate that generally LEO plasma will not be isothermal.
In eval_2Dpot_GS.m you set the neumann boudary conditions around the border as follows.
%set boundaries
b(1:nx) = 0; %zero electric field on y=0;
b(nn-nx+1:nn) = 0; %zero electric field on y=L;
b(nx:nx:nn) = 0; %zero electric field on x=L;
b(1:nx:nn) = phi0; %fixed potential on x=0;
But in flow_around_plate.m you set the electric field around the border as follows.
efx(1,:) = 2*(phi(1,:) – phi(2,:)); %forward difference on x=0
efx(nx,:) = 2*(phi(nx-1,:) – phi(nx,:)); %backward difference on x=Lx
efy(:,1) = 2*(phi(:,1) – phi(:,2)); %forward difference on y=0
efy(:,ny) = 2*(phi(:,ny-1) – phi(:,ny)); %forward difference on y=Ly
Should the normal electric field on the borders y=0, y=L, x=L just be set to zero to match the boundary conditions?
efx(nx,:) = 0;
efy(:,1) = 0;
efy(:,ny) = 0;
Great example! Thank you.
I downloaded all files and ran them at the Octave. I received strange results: at every time step I have 0 particles and blank graphic.
Have you any suggestions about how I can solve my problem?
I’m sorry for dumb question..
I found where was a problem.
I downloaded all files and ran them at the Matlab. At every time step I have 0 particles and blank graphic.
Hi Sudhan, thanks for catching this. The equation for thermal velocity must have gotten screwed up at some point. I fixed it. Try it again and let me know if it still doesn’t work.
Thanks for your sharing. I was looking for MPM on the website to solve some normal fluid problems. Then I got here. I saw some interesting results from MPM, for example: http://grantkot.com/MPM/Liquid.html. Interesting, haha.
Thanks for the link!
Is it possible to incorporate magnetic field to this code??
Another thing, How I can plot the velocity distribution of the particles from this code?
Yes, you can have a static magnetic field. See the article on the Boris method for details of implementing the particle pusher.
You will generally need to write your own code to compute the VDF. Just create a number of bins and iterate over the particles and increment the bin counters based on their speed. Then you can normalize the bins if needed by the max value or the sum.
I have tried to plot the electric field using quiver command from the data efx and efy and got a result. Problem is that I am getting a swirl kind of structure in the electric field. which is not acceptable as i have also introduced two parallel plates instead of one. One I have kept at y=Ly and another at y=0. having width $ \delta $ x = 3
Hi, first of all I would like to say this is a great blog. I had been reading and testing some of the codes you posted here.
I am doing a thesis on an inertial electrostatic confinement reactor (basically have to model flow of plasma due to a static electric field). I have two concentric (mostly transparent) grids held at about 60KV potential. Gases are ionized at the outer grid and accelerate towards the central grid. In the center some undergo fusion. Ions will also undergo recirculations (if they don’t collide with the central grid).
So I am wondering if it will be possible to alter the geometries of this code (perhaps 2D circular geometry), and have grids rather than plates? Would it be viable to model an IEC device using this method? I would greatly appreciate any help you can provide.
Kind regards,
Jimmy Zhan
Hi Jimmy, you should check out our Starfish code (still in development). It is a general 2D solver that can be used for a number of different geometries.
Great blog,I have been working on the codes posted here. The link you posted here was very useful.I am learning plasma out of interest. Thank you so much.
How this particle in cell simulation may be used for “self-focusing of laser beam in plasmas”
Hi,
This is really a very fascinating site on PIC. With the above example of 2D PIC, is it possible to calculate current recorded by the plate as a function of time ? Can we use the formula (charge hitting the plate in time dT) / dT to calculate current at a particular time instant ? Since it is a 2D simulation, what will the current mean physically ? Is this the current collected by a plate of given x and y dimensions but with UNIT DIMENSION along Z (i.e. 1 meter) ? Your thought on this will be very helpful. Thanks!
Hi Prakash, yes, you would basically count the number of particles hitting the plate and average over some time. Since this is an ion-only simulation, you will also need to include the electron term, which for can be modeled analytically from the planar sheath equation. For a 2D XY simulation like this one, the current will be current per unit depth as you mentioned. If this were an axisymmetric simulation, then you could compute the actual surface area by considering the body of revolution.
Thanks a lot. This is the only elaborately-explained resource on the web on Particle-In-Cell. Please keep it up.
Hi,I would like to say this is a great blog. It helps me a lot in my final project.
I have tried to understand your code. About Debye length calculation,I could not understand lD = sqrt(EPS0*Te/(n0*QE)); %Debye length. According to formula, I thought is lD = sqrt(EPS0*Te*K/(n0*QE*QE)). Can you explain it, please? Thank you!
Hi Helen, this is because in the above example, electron temperature Te is in electron volts. The conversion from Kelvin to electron volts is k*Te(K)/QE = Te(eV).
Thanks,Lubos. Can i ask about u=(j-1)*nx+1? what is this for ?
hi
can i use this code for higher densities (about 10^20 #/m^3) ?
is this code suitable for tokamak plasma simulation?
Hi Lubos,
I’m interested to particle in cell LINAC (linear accelerator) application where it used protons charges. Is Your matlab code adapt for this application? However I have a series coupling resonant cavity where the proton beam through it. For example initial energy is 7 MeV and the cavity were designed to accelerate untill 10 MeV.
Thank
Hi lubos,
I faced one problem to understanding the 2 lines
A(u,u-nx)=1/(dh*dh); %phi(i,j-1)
A(u,u+nx)=1/(dh*dh); %phi(i,j+1)
why you take ‘u’ constant for j ? and why you use ‘u-nx’ and ‘u+nx’?
kindly waiting for your reply
Hi Hiral, this is the “y” derivative part of the laplacian, $latex \nabla^2 \equiv (\partial^2/\partial x^2 + \partial^2/\partial y^2)$. The phi data is actually a 2d matrix. However, in order to perform a matrix-vector multiplication, this 2d data needs to be flattened into a 1D array. One way of doing this is to take all the values for j=0 (such as phi(1,0), phi(2,0),.. phi(nx,0)) followed by the values for j=1, etc… Using this scheme, a value corresponding to (i,j+1) will be located nx entries away from (i,j). If u corresponds to the value at (i,j), then (u+nx) will correspond to the value at (i,j+1). The actual computation is u=j*nx+i.
Hi Lubos,
Thanks
I am trying to make PIC for Lunar model using coulomb’s Law. But, I am confusing with output value of force. I am sending that matlab file on Email ID. Please, kindly inform me the solution.
hi Lubos
Here, “phi” – is surface potential or electron potential? and also “den”- is electron density?
Kindly waiting for your replay.
hi Lubos,
I want to simulate the same problem using circle instead of Rectangular plate..What changes I can do??
Waiting for our reply..
Hi Zarana, you have basically two options. You can either write the code in 3D, or you can implement an axisymmetric (RZ) version of the code. The second is probably what you had in mind. Looking at the blog now, I just realized that I don’t think I have a post on an RZ PIC code. I will try to post it over the weekend.
Hi Lubos.
please can u help me with the code to simulate particle (e.g Red Blood cell) trajectories in micro channel (e.g Deterministic lateral displacement).
I will appreciate any assistance rendered.
Hi Daniel, I sent you an email but replying here as well in case you didn’t get it. Can you email me more info on what you are trying to do?
Hi Lubos, How do those neumann and dirichlet boundary conditions in the code work.
For example, in
for i=1:nx
u = i
A(u,u) = -1/dh;
A(u,u+nx) = 1/dh;
end
How are the values for A(u,u) and A(u,u+nx) formulated?
That just means -phi[i][j] + phi[i+1][j] = 0, or d(phi)/dx = 0, since on the boundary d(phi)/dx is estimated as (phi[i+1][j]-phi[i][j])/dx.
But in the comments you mention that
A(u,u) refers to phi(i,j), and A(u,u+nx) refers to phi(i,j+1). That would refer to the element right above y=0, not the one right next to phi(i,j)? Am I confusing something here?
Actually, I think I figured out why it works that way 🙂 Thanks you!
I know nothing about PIC, but the instructor of a plasma related course told us to write a code of “PIC simulation of 1-D collision-less argon gas discharge”, including a model where the ions move and one that the ions don’t as our final project. A few different sets of data are required, like V-x, E-x, Ion density-x and so on. A lot of my classmates are as perplexed as me, as we have no prior experience with this type of work. Could you please be so kind and help me out?
Also, I can’t seem to run the example codes on this page with MATLAB.
Hi Dan, I responded to you through email. Check your spam folder if you don’t see it.
Hi Lubos,
In the potential solver code, what exactly is the following doing (I get it that from your comments you are setting up the boundaries, but am having difficulty visualizing it, given the notation used).
b(1:nx) = 0; //Rows 1 to 13 have value 0?
b(nn-nx+1:nn) = 0; //Rows 157 to 169 have value 0?
b(nx:nx:nn) = 0; // .. ?
b(1:nx:nn) = phi0; // .. ?
Thank you!
Hi Lubos, I’m a rookie in PIC simulation
The Leapfrog method is commonly used in PIC codes. The Leapfrog method is commonly used in PIC codes. The times at which velocity and positions caculated are offset from each other by half a time step. As such, the two quantities leap over each other.
I want to know how to move V(0) backword half a time step to V(-dt/2). As such, the two quantities leap over each other.
I want to know how to move V(0) backword half a time step to V(-dt/2).
Using backward-difference :V(0)-V(-dt/2)=E(0)*dt/2 ?
Hi lubos
which code of pic simulation is suitable for laser driven accelerator? can I buy it? how can I access that?
Thank you
Hi Lubos,
Just a quick question. For the Right hand side of our defining equation you have -e/eps(n(i) – n(0)exp(phi/kTe)).
In the code, in eval_2dpotGS you use
b = b0 – n0*exp((x-phi0)/Te);
where b0 = reshape(den) etc.
Does this mean you are not considering the ion motion, and only the electrons?
Hi Ajay, the ion charge density is obtained from the particles, by scattering them to the grid. That’s what gives the “den” term. The n0*exp(..) term is the density of electrons from the Boltzmann relationship. Since charge density is number density times charge, you have rho = q*(den_i – den_e), assuming singly charged ions.
Thank you!!! these is a great work!
many questions 🙂
what means 1D for the cell size? or what are the dimensions of the plate?
why there is ion density inside of the plate? I guess is for the type of border condition, but still I dont understand, is not possible to put some kind of step function on that border, not just a point where is zero, but beyond as well?
where the data get stored? there is a way to print in a file the density and potential matrices?
if I want to have only ions, I put the temperature(or density) of the electrons very small?
what is the difference between Ti and v_drift ?
I am running octave-gui on windows 10, and so far so good!
Thanks!
Enrique, let me try to answer your questions:
1) lD is Debye length. The Poisson solver may have convergence problems if the cell size is bigger than this. This is because we don’t resolve non-neutrality if cells are greater than the Debye length. The box just spans 1/2 of the height.
2) There isn’t. It’s a plotting issue. Density is stored on the nodes, and there is a node at the box outer surface. So you have one node with some finite value and another on the right with zero. The contour plotter fills the gap in between by linearly interpolating from the value down to zero.
3) Sure, you can export the results to a file. This was just a simple Matlab example. If you for instance check out the more recent finite element PIC example, you will see that one exports to a file and Paraview is used for plotting.
4) You could just set the n0 Boltzmann relationship term to zero. But this will likely result in very high potentials / the solver diverging / particles flying at crazy velocities.
5) Vdrift is a constant velocity. Ti controls the ion temperature. Gas temperature is basically the spread in velocities. So if Ti was zero, all ions are born with v=v_drift. The non-zero Ti then adds some random component to the velocity.
Hopefully these helped!
thank you that was very helpful
Hi, thanks for your support in this interesting topic. I have a problem with the eval_2dpot_GS.m file,
Error using eval_2dpot_GS (line 20)
Not enough input arguments.
The line mentioned is:
x = reshape(phi, numel(phi),1);
I tried writing phi0 instead of phi and pass it through, but then appears another mistake in the line
x(i)=(b(i) – A(i,1:i-1)*x(1:i-1) – A(i,i+1:nn)*x(i+1:nn))/A(i,i);
Problaby is for my version of matlab, (2014), but Im not sure. It seems that are kind of basic mistakes, but I dont have the expertise to solve it.
thanks if you can help.
Hi Lubos,
I have been trying out different values for the parameters used in the code. Is there a lower limit to the values used for v_drift?
For example, when I tried using a value of 990 m/s, while my graph for the electric potential was quite similar to that in the case of v = 7000 m/s, my density graph was quite messed up.
I was wondering if this was an inherent limitation of the code?
Thanks for your time.
Hi Ajay,
I wonder if this is due to thermal velocity becoming larger than the drift velocity. In that case you may end up with newborn particles moving in the -x direction. Ideally the code would check for this and reflect them but that is not implemented as the code assumes that v_drift>v_th.
Hi Lubos,
Why exactly are we requiring that v_drift > v_th. does this condition follow upon the nature of ion speeds particularly in the case of thrusters and such?
Hi,Lubos
I am just remaking flow_around_plate.m and eval_2dpot_GS.m. from ‘download’ site.
But, following error has been happened.
error==>minus
matrix unmatched
error==> eval_2dpot_GS at 22
b = b0 – n0*exp((x-phi0)/Te); %add boltzmann term for electrons
error==>flow_around_plate at 136
phi = eval_2dpot_GS(phi);
How can I solve this problem.
regards,
Keiichi Tanaka(26/Oct/2016)
Hi Keiichi, what program are you using to run the example? I don’t have Matlab so I tested the code with Octave. I just ran it and it ran fine.
How can we follow the trajectory of a particle
You can generate a trace file to which you would output position (and possibly velocities) of the same particle. If you are storing your particles in an array, you would do something like:
p = random(num_particles)
//main loop
- update e field)
- push particles
- output pos[p], vel[p]
I am simulating on deuterium-tritium plasma heating due to nonlinear plasma interaction will pic be useful?. Also i had problem of assigning charge density on grid via weighting procedures(cic)how can this be done so that one solves the poison equation?
This really depends on the plasma density. Generally, PIC is more suitable to lower density plasmas. Using PIC for high density discharges (like in fusion) typically requires a prohibitively large number of particles and mesh cells.
can you suggest to me a more realistic approach to this problem please
I want to use pic code for the study of magnetic reconnection in astrophysical plasma. I have few questions about it. 1. Can I use your code in this context? 2. What are the boundary conditions and potentials applicable for it? 3. Can you suggest some simple examples of reconnection simulation in PIC?
Hello Sir,
Can I know what are the interpolation techniques used for grid to particles and particle to grid interpolation?
In the Poisson solver, the boundary conditions are set in b – the RHS vector. Shouldn’t it be on x – the potential?
I tried to replace the b by x in the boundaries in eval_2dpot_GS.m but get errors.
Could you please clarify?
With a matrix solver, you solve for all rows in the “x” vector. In order to get fixed values, you set the corresponding coefficients in the A matrix and the RHS such that the appropriate equation reads: “1*x=b”. This then gives the fixed value “x=b”. Similarly for a Neumann boundary you would have something like “x[0] – x[1] = 0”, which implies that x[0]=x[1].
when i run the above code in octave it gives me an error
“error: ‘eval_2dpot_GS’ undefined near line 44 column 11 ” ..
And is there any way to compliment this way in c++ rather than matlab ?
I am getting the following error using a online Octave compiler
$octave -qf –no-window-system demo.m
Solving potential for the first time. Please be patient, this could take a while.
warning: function ./demo.m shadows a core library function
error: ‘eval_2dpot_GS’ undefined near line 165 column 11
error: execution exception in demo.m
Dear professor,
I am now studying FEM-PIC code, it can running well with PLASMA_DEN=10e10.
But, with PLASMA_DEN=10e14 or higher, there is error when running.
With possible reasons, I do my best to read in details. But, still there is error.
I wish getting your help.
Thank you very much.
How would one deposit and interpolate charge on the grid in one dimension whereas your code is 2d.
since I’m a new in using
pic
Can you please suggest me how to reconfigure the code, to model an electron flow around an spherical object?
I am a new user in MATLAB.
Could you tell me, please, can I use MATLAB for LASER plasma interaction? Please, help me.
plz help me. I am trying to solve 2d3v problem in matlb by using pic simulation which book should I follow. I want to learn from basic about pic simulation.