Computing pi with CPUs, GPUs, threads, MPI, Javascript, Arduino, and FPGAs

This year, for “pi day” (March 14th), I figured I’ll post a short article demonstrating how to estimate the value of π using different computer architectures. This topic is somewhat in line with the ASTE-499 Applied Scientific Computing Course I am currently teaching at USC’s Astronautical Engineering Department. The goal of that course is to […] (Mar 14 2020)

Introduction to Vlasov Solvers

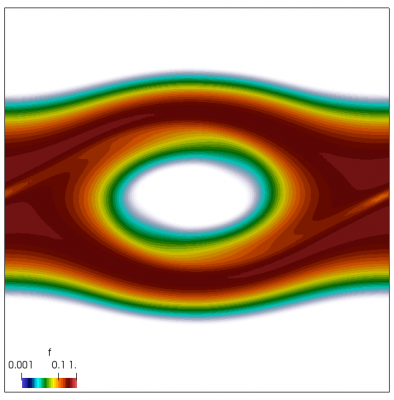
A simple 1D-1V Vlasov code for two-stream instability is developed. The code is based on a splitting scheme proposed by Cheng and Knorr in 1975. (Sep 11 2018)

Vorticity – Stream Function Formulation for Axisymmetric Flow

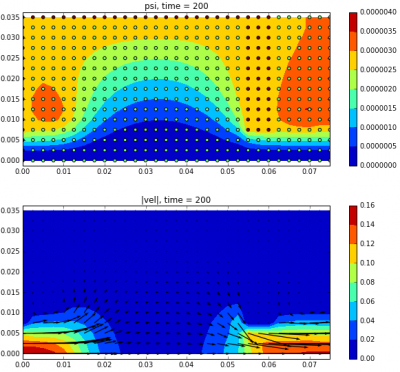
Vorticity - Stream Function formulation for incompressible Navier Stokes equation is developed and demonstrated with Python code for flow in a cylindrical cavity. More complex geometry from a Java code is also shown. (May 27 2016)

Brief Intro to GPU PIC with CUDA

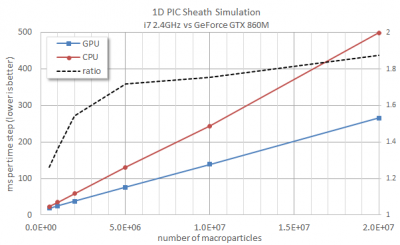
This post shows how to develop a PIC plasma simulation code that uses NVIDIA CUDA to perform computations on the graphics card (GPU). Even without any optimization, the GPU version runs almost twice as fast as the CPU version for a large number of particles. (Feb 25 2016)

Finite Element Particle in Cell (FEM-PIC)

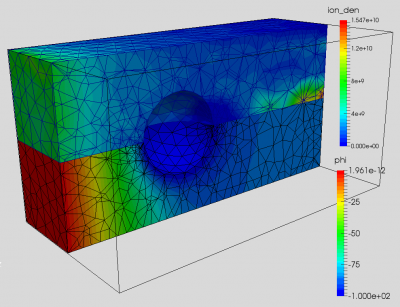
Example Finite Element Particle in Cell code for flow of ions past a charged sphere on an unstructured mesh (Dec 23 2015)

Particle In Cell Method in Cylindrical Coordinates

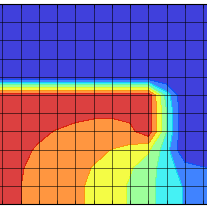
Details of implementing plasma simulations with the Particle In Cell Method in cylindrical coordinates. We develop a simulation of a simplistic ion gun. (Jun 15 2015)

Stretched Mesh

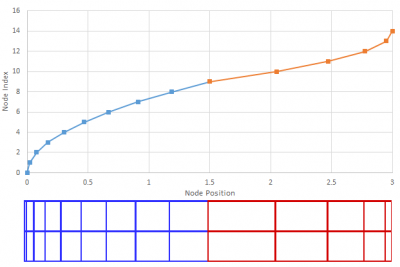
Tutorial on implementing mesh stretching in Particle In Cell codes. Equations for node positions and finite difference coefficients are derived. (Feb 18 2015)

Flow in a Nozzle

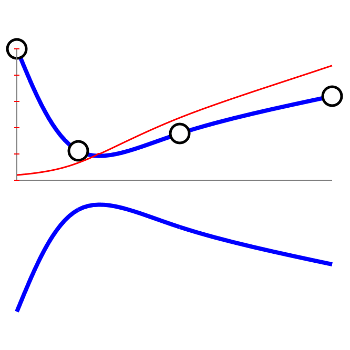
By considering one-dimensional flow, we can derive an expression for the variation of Mach number in a nozzle with a variable area change. Such a relationship is explored here with an interactive demo that allows you to change the shape of a converging-diverging nozzle and observe how the flow speed changes. (Feb 7 2014)

Computing Intersections Between a Cubic Bezier Curve and a Line

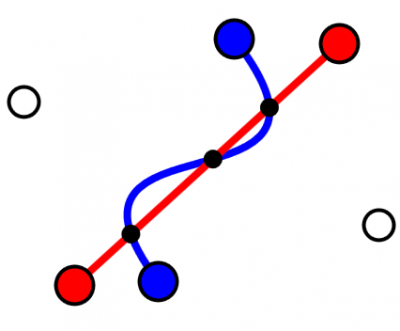
Interactive SVG+Javascript code for computing intersections between a line and a cubic Bezier curve. (Aug 10 2013)

Bird’s DSMC0.FOR in Java

G.A. Bird included several example codes with his book on the DSMC method. These codes are written in Fortran 77 which makes them somewhat hard to understand due to short variable names and reliance on global variables. This post is a summary of my effort to convert DSMC0.FOR to Java. (Jun 29 2013)

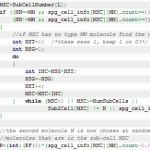
Efficient Particle Data Structures

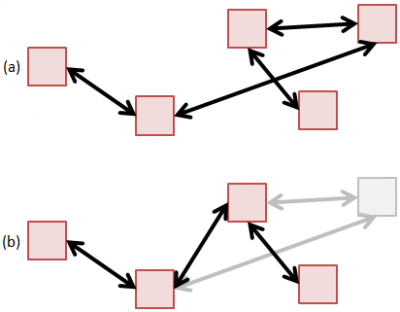
Particle codes have very different memory optimization requirements than fluid-based solvers. Here we consider three types of data structures for holding particles that offer an efficient way of adding and removing particles and compare their performance. (Jun 11 2012)

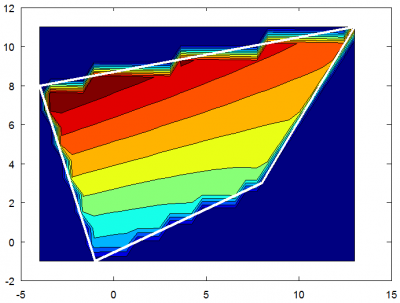
2D Finite Element Method in MATLAB

This tutorial discusses how to generate unstructured meshes using a Matlab code distmesh.m and how to use the mesh in a Matlab Finite Element Solver to solve the Poisson's equation on an unstructured domain. (Jun 8 2012)

Interpolation using an arbitrary quadrilateral

This article describes how to interpolate data between a particle and an arbitrary quadrilateral cell used in non-Cartesian grids. The technique is illustrated with several Matlab / Octave examples. The examples show how pick points located inside the polygon, how to classify their position, and how to scatter and gather particle data. (Jun 4 2012)

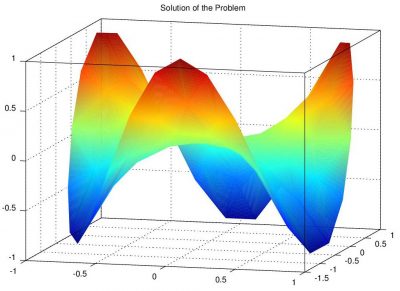
Nonlinear Poisson Solver

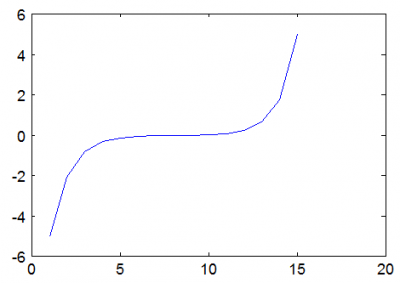
Nonlinear Poisson's equation arises in typical plasma simulations which use a fluid approximation to model electron density. This article describes how to solve the non-linear Poisson's equation using the Newton's method and demonstrates the algorithm with a simple Matlab code. (Apr 30 2012)

Code Optimization: Speed up your code by rearranging data access

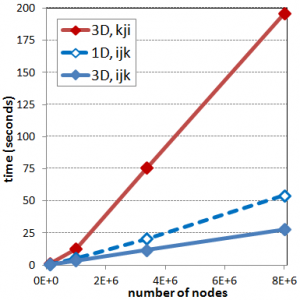
Often, a significant code speed up can be accomplished by simply rearranging the way data is stored or accessed in memory. This article compares data access with arrays vs. linked lists, and compares loop ordering for 3D data sets. It also looks at a flat 1D array representation of 3D data via a mapping function. (Apr 22 2012)

Orthogonal Curvilinear Coordinates

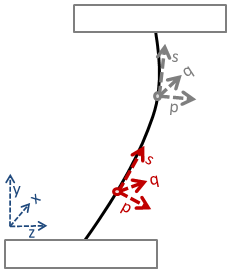
Cylindrical and spherical coordinates are just two examples of general orthogonal curvilinear coordinates. In this article we derive the vector operators such as gradient, divergence, Laplacian, and curl for a general orthogonal curvilinear coordinate system. (Jan 16 2012)

Simple Particle In Cell Code in Matlab

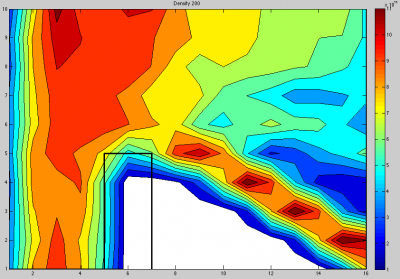
This article includes the source code for a simple particle in cell code. The code simulates flow of plasma over a charged plate and is written in Matlab. (Nov 28 2011)

Multiscale Modeling of Hall Thrusters

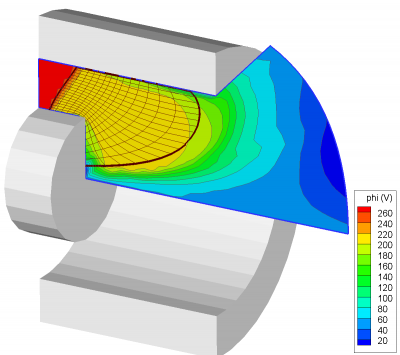
One of the topics we specialize in at Particle In Cell Consulting is modeling of electric propulsion (EP) thrusters. These devices generate thrust by accelerating ionized propellant (plasma). One of the most efficient EP devices is the Hall thruster. These devices have been flown for over 40 years, however, much still remains unknown about the details of their operation. (Aug 24 2011)

Get results faster with Java multithreading

Code parallelization is the process of modifying a simulation program so that it can take advantage of multiple computational cores to obtain results faster. One method is to distribute the workload locally in the form of computational threads. Java makes it easy to add multithreading to your code. Here we show you how to implement a "poor-man's" method, in which individual cases run serially, but multiple cases are launched concurrently. (Jun 25 2011)

The Finite Volume Method

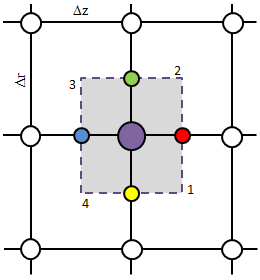
The Finite Volume Method (FVM) is an algorithm for solving differential equations. It is based on the integral formulation of the problem, with each computational element corresponding to a volume over which the integration is performed. It is somewhat more complex than the Finite Difference, however, it can be applied to arbitrarily shaped domains. In this article we show you the basics of this method and provide a simple solver. (Apr 19 2011)

Posts in Category Numerical Methods